30863 img067 (21)

72

Równanie Newtona-Raphsona dla układu równań (3.116) nie jest w tym przykładzie określone w całej przestrzeni R², ponieważ macierz Jacobiego .// (x) nie jest macierzą nieoso-bliwą dla wszystkich punktów x e R². Jest ona macierzą osobliwą w punktach, w których

72

det

2x_x

1

2x₂

-1

-2 • (x_t + x₂) = 0,

(3.120)

a więc w punktach (x_x,x₂) e R² o współrzędnych spełniających równanie x_x + x₂ = 0. Pełny wzór opisujący iteracje ma postać

^x2,(o)

^xl,(/t+l)		’^xa*)l	1 +	-1	2^2 ,(k)	^x\{k) ^+ x2,(k)^
_^x2,(k+l)_		^x2{k)_	2 ' (Xl,(i) + ^x2,{k))	-1	2^xi ,(t)	^X\,(k)~^X2,(k)

(3.121)

Wykonując eksperyment numeryczny, otrzymuje się we wniosku, że ciągi iterowane dane formułą rekurencyjną (3.121) algorytmu Newtona-Raphsona są zbieżne do jednego z punktów x*' lub x*", dla każdego punktu początkowego x₍₀) dla iteracji należącego do podzbioru R² \{(xi, x₂) e R²: x_x + x₂ = 0} przestrzeni R². Dla każdego punktu początkowego (xi_i(0), X2,(0)) o współrzędnych spełniających relację x₂,(o) > -Xi,(o> odpowiedni ciąg iterowany jest zbieżny do punktu x*', natomiast dla każdego punktu początkowego (xi ₍₀), x₂,(o)) o współrzędnych spełniających relację x₂,(o) < -xi,(o> odpowiedni ciąg iterowany jest zbieżny do punktu x*". Obszary przyciągania dla ciągów iterowanych przez każdy z punktów x ' i x " zaznaczono na rys. 3.13.    ■

Przykład 3.6

(x* ,x₂)=

(*r >^x2 )=

x,² + x\ - 1 = Oj

2    f ⁵

x₂ - Xj =0

(3.122)

gdzie (xi, x₂) e R . Jego rozwiązaniami są następujące dwie pary liczb:

i    >

V-2 + 2V5 -l + yj 2 ’ 2

V-2 + 2V? -1 + V5

(3.123)

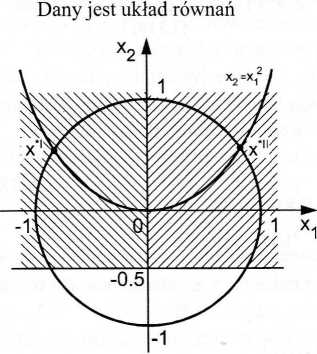
Rys. 3.14. Rozwiązania układu równań (3.122)

Rozwiązania układu równań (3.122) określają współrzędne wyznaczonych graficznie na rys. 3.14 punktów x*' ix*".

Wzór rekurencyjny (3.96) dla iteracji Newtona-Raphsona przyjmuje postać