49079 P1080232

4. Wprowadzenie do kinematyki robotów

4.3.2. Kinematyka manipulatora równoległego typu hexapod

Do rozwiązania zadania prostego manipulatora równoległego typu hexapod 6-3 stosuje się metodę wektorową. Wektorami platformy są: P\₀, P₂o i P30, jak poka. zano na rys. 4.22.

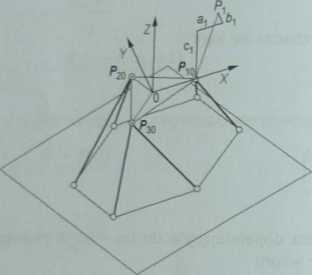
Rysunek 4.22_

Struktura geometryczna hexapoda 6-3

Platformę roboczą tworzy trójkąt równoboczny o boku L. Wtedy długości wektorów OPn (dla /= 1,2,3) wynoszą

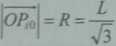
(4.60)

Kiedy wektory platformy przemieszczają się z P*, do P„ wtedy

Pi — Pio + AP/ = Pn + di + bi + c_f    ’’    (4.61)

gdzie: a„ b, i c, są przesunięciami punktu P*, wzdłuż osi X, Y, Z.

Dla przesunięcia stałe są długości boków trójkąta równobocznego, jaki tworzy platforma. Z tego wynika

I Pi-P_t MPio-Pjo P    I I I (4.«)

gdzie: i,j brane są w porządku cyklicznym. Stąd wynika równanie

2\P,o-P,o\|A/>₍-AP,| + |AP,-AP_yp=0    ‘    (4.63)

które następnie jest przekształcane do postaci

\2Pjo- AP -2P_l0 - \Pj -2P_/0 AP, + 2P_j0 -APj | + AP? -2AP, ■ AP, + AP? = °

f (4.64)

W równaniu tym można uwzględnić wektory a,-, &; i e„ wtedy kilka wartości iloczynów skalarnych można usunąć z powodu prostopadłości. Pozostałe kąty mają wartości 0°, 30°, 120° i 210°. Po wstawieniu wartości cosinusów i kilku uproszczeniach otrzymuje się równanie

a]+a'j —j=[(bl -bj)—(-j3a'i -b'j){4?>a'j-b'j)-(a\ - a))² -{b]+b'j)²-{c\ -c))²]

(4.65)

gdzie

, _^ai

(4.66)

Dla małych przemieszczeń wartości powyższych wyrażeń są bliskie jedności.

a)

p

b)

p

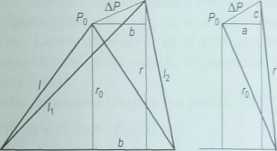
Rysunek 4.^____

Geometria pary kończyn hexapoda

Na rysunku 4.23 przedstawiono pary kończyn w rzutach na płaszczyzny YZ i XZ. Biorąc pod uwagę trójkąty l\r i Ur na rys. 4.23a oraz używając twierdzenia Pitagorasa, można otrzymać równania

ó"=I(/"²-#²)=(A/r- a/d i+—(A/r+Af)

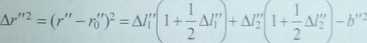
(4.67)

(4.68)

gdzie

/

(4.69)

Z trójkąta prostokątnego zawierającego bok r (4.23b) można ułożyć równanie

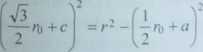
(4.70)

111