52449 Untitled Scanned 66 (3)

4. STEREOMETRIA

CZĘŚĆ TEORETYCZNA

KĄT MIĘDZY PROSTĄ I PŁASZCZYZNĄ

* Prosta /jest prostopadła do płaszczyzny P. jeśli jest prostopadła do każdej prostej zawartej w płaszczyźnie P mającej punkt wspólny z prostą /.

•fr Jeśli prosta / nie jest równoległa i nic jest prostopadła do płaszczyzny P. to kątem nachylenia prostej / do płaszczyzny P nazywamy kąt między prostą / i jej rzutem prostokątnym na płaszczyznę /’ (rysunek obok).

TWIERDZENIE O TRZECH PROSTYCH PROSTOPADŁYCH

■=> Niech k będzie prostą, która nic jest równoległa i nie jest prostopadła do płaszczyzny P, a / prostą zawierającą się w płaszczyźnie P i przechodzącą prze/, punkt wspólny prostej k i płaszczyzny P. Prosta / jest prostopadła do prostej k wtedy i tylko wtedy, gdy / jest prostopadła do rzutu prostokątnego k' prostej k na płaszczyznę P (rysunek obok).

KĄT DWUŚCIENNY

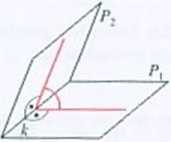
o Niech a oznacza kąt dwuścicnny wyznaczony przez różne półpłaszczy-zny P\ i Pi mające wspólną krawędź k. Miarą kąta a nazywamy miarę wypukłego kąta płaskiego, którego wierzchołek należy do prostej k, a ramiona są prostopadłe do k i jedno z nich zawiera się w pólpłaszezyź-nie Pu a drugie w półpłaszczyźnie Pi (rysunek obok t.

GRANIASTOSŁUPY

Równolcgłościan - graniastosłup, którego podstawą jest równolcgłohok.

*♦ Graniastosłup prosty - graniastosłup, którego krawędzie boczne są prostopadłe do podstaw.

Graniastosłup prawidłowy - graniastosłup prosty, którego podstawa jest wielokątem foremnym.

*    Prostopadłościan - graniastosłup prosty, którego podstawa jest prostokątem.

Objętość graniastosłupa o polu podstawy P i wysokości h: V= PU.

*    Pole powierzchni całkowitej: P,-P,, + 2P </**. - pole powierzchni bocznej, P - pole podstawy graniastosłupa).

OSTROSŁUPY

*    Ostrosłup prawidłowy - ostrosłup, którego wszystkie krawędzie boczne są równe, a podstawa jest wielokątem foremnym. Czworościan foremny - ostrosłup, którego wszystkie ściany są trójkątami równobocznymi.

Spodek wysokości ostrosłupa - rzut prostokątny wierzchołka ostrosłupa na płaszczyznę podstawy.

*    Twierdzenia o ostrosłupach.

11 Jeśli wszystkie krawędzie boczne są równe (lub jeśli wszystkie krawędzie boczne tworzą z płaszczyzną podstawy równe kąty), to na podstawie ostrosłupa można opisać okrąg, którego środkiem jest spodek wysokości ostrosłupa.

Jeśli wszystkie ściany boczne tworzą z podstawą równe kąty. to w podstawę ostrosłupa można wpisać okrąg, którego środkiem jest spodek wysokości ostrosłupa.

=> Objętość ostrosłupa o polu podstawy P i wysokości h: V = -j Ph.

Pole powierzchni całkowitej: P_r = P,, i P, gdzie P_t, jest polem powierzchni bocznej, a P polem podstawy ostrosłupa.

WALEC

Oznaczenia: r - promień podstawy walca, h - wysokość walca.

*> Objętość: V-nrh. => Pole powierzchni bocznej: P_h=2Krh.    Pole powierzchni¹ całkowitej: P_e = 2nr(r+h).