56789 skanuj0348 (2)

Wytrzymałość pasów. Naprężenia w pasie są wywołane działaniem su (napięć) rozciągających, zginających oraz sił bezwładności, powstających poć wpływem siły odśrodkowej.

Naprężenia rozciągające, powstające pod wpływem napięcia F_ oblicza się z ogólnej zależności

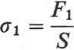
(13.17)

Naprężenia zginające występują w pasie w czasie jego wejścia i schodzenia z koła pasowego. Zakładając, że odkształcenia wywołane zginaniem mieszczą się w granicach odkształceń sprężystych, wartość naprężeń zginających w pasie można obliczać na podstawie prawa Hooke’a

Dą-g~    d    (13.18)

gdzie E_g — moduł sprężystości pasa przy zginaniu (tabl. 13.1).

Przyjmując wartość przybliżoną wzoru 13.18, otrzymuje się większą wartość naprężeń zginających w granicach kilku %, a zatem wpływa to korzystnie na obliczanie wytrzymałości pasa. Z zależności 13.18 wynika, że największe naprężenia zginające występują na małym kole. W celu zabezpieczenia pasa przed zbyt dużymi naprężeniami, a tym samym przed zbyt szybkim zużyciem, należy dążyć do tego, aby stosunek g/D był możliwie mały.

Obciążeniem powodującym powstanie w pasie dodatkowych naprężeń rozciągających są siły bezwładności (siły odśrodkowe) F_b. Do obliczania napięcia pasa siłą F_b oraz naprężeń z nią związanych służą zależno-

ści:
Fb = 6- S-v2 w N	(13.19)
oraz
Fb c 2 d ab = — = o • v w Pa	(13.20)
w których: 3 — gęstość materiału pasa w kg/m^2, S — pole przekroju pasa w m^2, v — prędkość pasa w m/s.

Wartość naprężeń a_b wywiera duży wpływ na wytrzymałość pasa przy v > 30 m/s. Przy prędkościach v < 10 m/s naprężenia te (w stosunku do i o_g) są bardzo małe i można je pominąć.

Naprężenia występujące wskutek rozciągania pasa (o^ i <r_b) oraz jego zginania (o_gmax) są naprężeniami normalnymi, zatem warunek wytrzymałościowy pasa przyjmuje postać

(Tl    (T1 (Tg max "ł” (T_b ^ k_r    (13.21)

348