61397 str043 (3)

4.1.3.3.1.2. Wy/nac/onlo współrzędny) li |imyi,|l w pomiarach kodowych

Wykorzystując zależność (4.15) znpls/myiównnnlnpniiidoodlagloścl dla momentu czasu ortiz I logo satelity. Po Iowo) stronie znajdu|c slip /mini/nim prze/, odbiornik pseudoodleglość, natomiast prawa strona równania zawiera trzy niewiadomo 8_V, 8„ .

p₍(0=^(OlfA8(0 •    (4.19)

I ’irnloważ R'(t) jest geometryczną odległością pomiędzy satelitą a odbiornikiem w momencie czasu t, odnieśmy ją również do niewiadomych współrzędnych odbiornika (x,y, z) zapisując pod postacią:

R‘(x,y, z,t)=y][x'_f(t)- x\+ [y'(t)~^J²+ k(O^- A² ,    (4-20)

gdzie:

y[U),y\(t)< ^::i(0 - współrzędne kartezjańskie położenia satelity w momencie wysłania sygnału, x, y, ?. - współrzędne kartezjańskie położenia odbiornika w momencie odbioru sygnału.

I )i rkonajmy spostrzeżenia, że niewiadome x,y, z, w powyższym równaniu, przedstawiono w nieliniowej formie. Stąd koniecznym jest przyjąć przybliżone współrzędne odbiornika x₀, y₀, z₀, któro z nieznanymi (prawdziwymi) współrzędnymi x,y,z powiążmy zależnościami:

x = ;c₀ + Ax,    (4.21)

y = y₀ + Ay ,    (4.22)

z = z₀ + Az .    (4.23)

Zauważmy, iż w wyniku powyższych relacji pojawiły się nowe niewiadome, A*, Ay, Az , których wyznaczenie jest równoznaczne z rozwiązaniem zadania nawigacyjnego określenia pozycji, Ola współrzędnych przybliżonych x₀, y₀, z₀ na ten sam moment obserwacji i zapiszmy, przoz analogię do (4.20) relację

(f)“*J’+ kJ²⁺1<-    (4.24)

gdzie:

A’!,( v₍|, .i*,,, I) - odległość geometryczna pomiędzy położeniem satelity na moment obserwacji a pozycją przybliżoną,

v,„ i'₀,- współrzędne kartezjańskie pozycji przybliżonej.

I unkcję opisaną zależnością (4.20) można rozwinąć w szereg Taylora wykorzystując relacje: (4 .'I) - (4.23) oraz zdefiniowaną w (4.24) odległość między satelitą a pozycją przybliżoną utrzymując postać:

R^l (x, y, z, /)= R'„ (x_a + Ax,y₀+ Ay, z₀ + Az, t)= R‘_o (x₀, y₀, z₀,t)+

,    ^ , ć'f(x₀,y₀,z₀)    _| df(x₀,y₀,z₀) ^ _|    (4.25)

&₀    qy₀ ’    Sz₀

tm

Rozpatrzmy pochodne

^(l/ (•*!!» jy*!) ).	x'A) *0	(4.20
	Kit)
^(?/ (Wo.^zo)_	yX<) y»	(4.27
	Ki>)
vf(^x<ny»,^zn)	z‘X)-zQ	(4.28

dz₀    R'₀(t)

które po podstawieniu do (4.25) sprowadzają funkcję do postaci liniowej

R'(x,y,z,t)= R‘Xx₀,y_n,z₀,t)-

Kit)

•Ax —

y‘Ąt)-y₀ A„

Kit)

Ay-

m)

•Az . (4.21

Przekształcając równanie (4.19) w oparciu o relację (4.11) otrzymamy

P,(0='^R'(^x:>^^z»'')^+c-⁵o(0-^c-⁵X0 -    (4.3<

a podstawiając w miejsce R‘(x, y, z, t) zależność (4.29) uzyskujemy

P,(0^=/?X-Wo’VO

+ c.6₀(t)-c-5‘(t)

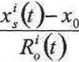
■Ax -

yX^[)-yo

KQ)

■Ay-

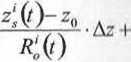
(4.3

Kolejnym krokiem obliczeniowym jest przeniesienie czynników z niewiadomymi na prawt| stroi a wiadomych na lewą. Stąd otrzymamy

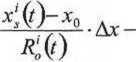
P, (0- K (*o ,y₀,z₀,t)+c-8'_s (t)=

■Ay-

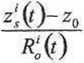
• Az + c-8_w(r)

y‘X^l)-yo

Kit)

Przeanalizujmy powyższe równanie. Lewa strona równania zawiera czynniki będące wtul ściami znanymi:

p,(0    - pseudoodległość, którą zmierzył odbiornik do i-tego satelity w momencie c/m

t,

R‘_a(xo, y₀, z₀, t) - odległość geometryczna między współrzędnymi satelity a przybliżoną pozyi odbiornika. Wyznaczenie współrzędnych kartezjańskich satelity umożliw transmitowanie danych w depeszy nawigacyjnej GPS. c-Q(t),    - błąd zegara i-tego satelity wyrażony w mierze odległościowej wyznaczany i

podstawie prezentowanych już zależności: (4.16) - (4.18).