67018 Scan0055

6.5 Zadania 67

Rozwiązanie:

•    funkcja nie jest injekcją, ponieważ istnieją takie X\,X2 6 R, że (xi ^ x₂) => [f (xi) = / (x₂)], na przykład x_x = -1, x₂ = 1,

•    funkcja nie jest surjekcją, ponieważ dla pewnych y nie istnieje takie x € R, że y = f (x), na przykład dla y — —4. Mamy tutaj Wj = (0, oc) = R₊ (zbiór liczb rzeczywistych nieujemnych), a nie R.

•    funkcja nie jest bijekcją, ponieważ nie jest injekcją (nie jest także surjekcją).

2. Dla danego przekształcenia / : R —» R zbadać, czy / jest injekcją. surjekcją i bijekcją. Jeżeli nie jest injekcją, podać x\ i X2 takie, że x\ 7^ x₂ i / (aą) = f (a^). Jeżeli nie jest surjekcją, podać Wf.

(a)

(b)

(c)

(d)

(^e)

(f)

(g)

/(*) = 2*

Odpowiedz: Funkcja jest injekcją i nie jest surjekcją. / (x) = x³

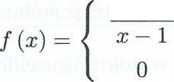
^2X + 1 dla x ^ 1 dla x = 1

Wskazówka: Wykorzystać własności funkcji homograficznej.

/ (x) = 2^X + x 2r

y/x + l 2x

/O) =

dla x ^ 0 dla x < 0

/ (x) = sina:

3.    Dana jest funkcja / : R —*• R, gdzie / (x) = sin2a; + 1. Wyznaczyć obrazy i przeciwobraz:

(a)    f(A), gdzie A = (0,tt)

(b)    f(A), gdzie A= {o,

(c)    /^_1 (B), gdzie B = {0}

Odpowiedz: f~¹ (B) = {a; : x = — j + kir. k G Z}.

4.    Niech / : R —> R, gdzie / (x) — a:² — 3a; 4- 2. Znaleźć obrazy i przed wobrazy: