73370 Str038 (2)

72 2. Ciulu ifcoltcronc I mety kwadratów*

Przykład 3. /a poniocą powyższego algorytmu znajdźmy pierwiastek kwadratowy z a « 186 modulo p - 401.

Rorwiąranic. Najmniejszą nicrcsztą jest n = 3. Mamy następnie /?- 1 = * 2⁴ • 25, a więc b — 3²⁵ = 268 oraz r = a¹³ = 103 (przy czym używamy znaku równości na oznaczenie kongrucncji modulo p). Po obliczeniu a~^l = 235, zauważamy, że r²/a - 98 musi być pierwiastkiem ósmego stopnia z jedności. Obliczamy 98⁴ = - 1, a więc j₀= 1. Następnie obliczamy (br)²/a = — 1. Ponieważ kwadrat tej liczby jest równy 1, więc mamy j\ = 0, a następnie j₂ = 1. Zatemj = 5 i szukanym pierwiastkiem kwadratowym jest b^sr = 304.

Uwagi:

1.    Jeżeli liczba pierwsza p przystaje do 3 modulo 4, to otrzymamy najprostszy przypadek powyższego algorytmu. Wtedy a=l, s = (p — l)/2, a więc (x + l)/2 = (p + l)/4 i widzimy, że już x - r = o^(p+1)/4 jest szukanym pierwiastkiem kwadratowym.

2.    Oszacujemy teraz czas działania tego algorytmu. Przypuśćmy, że rozpoczynamy obliczenia wiedząc już, że liczba n jest nieresztą. Wtedy znalezienie s, b i r = A^(,*^1)/2 (oczywiście modulo p) wymaga co najwyżej O (log³/?) operacji na bitach (por. twierdzenie 1.3.6). Zatem w procesie znajdowania j najbardziej czasochłonne jest podnoszenie pewnej liczby do potęgi 2^a~^k~² w jfc-tym kroku indukcyjnym, a to wymaga et — k — 2 podnoszeń do kwadratu modulo p, liczb mniejszych od p. Ponieważ et — k — 2 <a, mamy oszacowanie 0(alog²/?) każdego takiego kroku. Ponieważ mamy et — 1 takich kroków, więc ostatecznie nasze oszacowanie wynosi O (log³/? + a²log²/?) = ■= <9(log²/?(log/? + a²)). W najgorszym przypadku (jeśli liczba p — 1 niewiele różni się od potęgi dwójki) jest to O (log⁴/?), gdyż a < log₂p = = O (log/?). Zatem, jeśli znamy nieresztę modulo /?, to możemy obliczyć pierwiastek kwadratowy modulo p w czasie wielomianowym (ograniczonym przez czwartą potęgę liczby cyfr liczby /?).

3.    Prawdę mówiąc, nie wiemy (chyba że założymy prawdziwość tzw. „hipotezy Riemanna”), czy istnieje algorytm pozwalający znaleźć nieresztę modulo p w czasie wielomianowym. Jednakże dla danej liczby e > 0 istnieje algorytm działający w czasie wielomianowym znajdujący nieresztę z prawdopodobieństwem większym niż 1 — e. Mianowicie, z prawdopodobieństwem 50%, losowo wybrana liczba n, 0 < n < p, jest nieresztą, a to można sprawdzić w czasie wielomianowym (por. ćwiczenie 17 poniżej). Jeśli powtórzymy to dla więcej niż log₂(l/e) losowo wybranych liczb n, to z prawdopodobieństwem większym od 1 - e co najmniej jedna z tych liczb będzie nieresztą.

Ćwiczenia

1. Sporządź tablicę zawierającą wszystkie reszty kwadratowe i niereszty kwadratowe modulo p dla p = 3, 5, 7,13,17, 19.

6. Oblicz sumę Gaussa G = J) ( — jf* ({jest tu pierwiastkiem stopnia q z je-

dności w ciele Fp,, gdzie p⁷ = 1 (mod q)) dla:

(a)    ? = 7,p = 29,/= 1,5 = 7;

(b)    ^ = 5, p = 19, /= 2, { = 2 - 4/, gdzie i jest pierwiastkiem wielomianu Jif²+1;

(c)    q — l,p— 13,/= 2, { = 4 + a, gdzie a jest pierwiastkiem wielomianu J² - &

7.    Niech m = a⁴ + 1, fl ^ 2. Znajdź dodatnią liczbę całkowitą x zawartą między 0 i ml2 taką, że jc² = 2 (mod m). Wykorzystaj to do znalezienia /2 w ciele F_p, gdzie liczba p jest jedną z następujących liczb: liczby pierwsze Fermata 17, 257, 65537; p = 41 = (3⁴ +1)/2, p = 1297, p = 1201. (Wskazówka: skorzystaj z dowodu twierdzenia 2.2.4.)

8.    Niech p i q będą dwiema liczbami pierwszymi takimi, itq = \ (mod p). Niech { będzie pierwiastkiem pierwotnym stopnia p z jedności w ciele

F_q. Znajdź wzór wyrażający pierwiastek kwadratowy z ^—Jp w ciele F, za pomocą

9. (a) Niech m = a^p - 1, gdzie p jest nieparzystą liczbą pierwszą i a > 2. Znajdź dodatnią liczbę całkowitą jc zawartą między 0 i m/2 taką, że

-1

.2

p (mod m). Wykorzystaj to do obliczenia V 5 w ciele F₃₁,

y —7 w ciele F₁₂₇, yl3 w ciele F_B191 i y -7 w ciele F_l093.

(b) Znajdź wzór na najmniejszą dodatnią liczbę całkowitą, której kwadrat

przystaje do Mersenne’a.

p modulo q, gdzie q = 2^P - 1 jest liczbą pierwszą

1801

2.    Przypuśćmy, źe p\V* *f 1, gdzie K;>i,

(a)    Skorzystaj z ćwiczenia 4 do podrozdziału 1.4, by dowieść, źe p = I (mod 2*⁺¹).

(b)    Skorzystaj z twierdzenia 2.2.4, by dowieść, źc p a 1 (mod 2**²),

(c)    Skorzystaj z (b), by dowieść, że liczba 2¹* + 1 jest pierwsza.

3.    Ile pierwiastków z jedności stopnia 84 istnieje w ciele mającym II³ elementów?

4. Udowodnij, że

jeśli p s 5 lub 7 (mod 8). 91

-2\ . . _M - = 1, jeśli

^? J

p s 1 lub 3 (mod 8), oraz

5. Oblicz

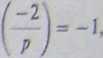
167

za pomocą prawa wzajemności.

10. Oblicz symbol Lcgendre'a ( J (a) korzystając z prawa wzajemności dla symbolu Legendre’a (tzn. rozkładając na czynniki wszystkie liczby