76199 ip1

Protokół z ćwiczenia : Identyfikacja modeli parametrycznych    da ta    . 4d..A ^ T

Laboratorium Identyfikacji Procesów    gmpa/sekcja....?J.=?..£r!..........................

lane Nazwisko ^ .—. , v . \L f-c? Cj_.jLz (Vłt tL- 'b 6 k-	.............75
Imię Ma s ko	.............75

Przebieg ćwiczenia

O.clJak można wykorzystać błąd predykcji do wyboru struktury modelu? (1.0 pkt) ,—

^    (A \*sv\    ,J_A oL_f

_Ł°    tWn^j moJó^f ^b    -

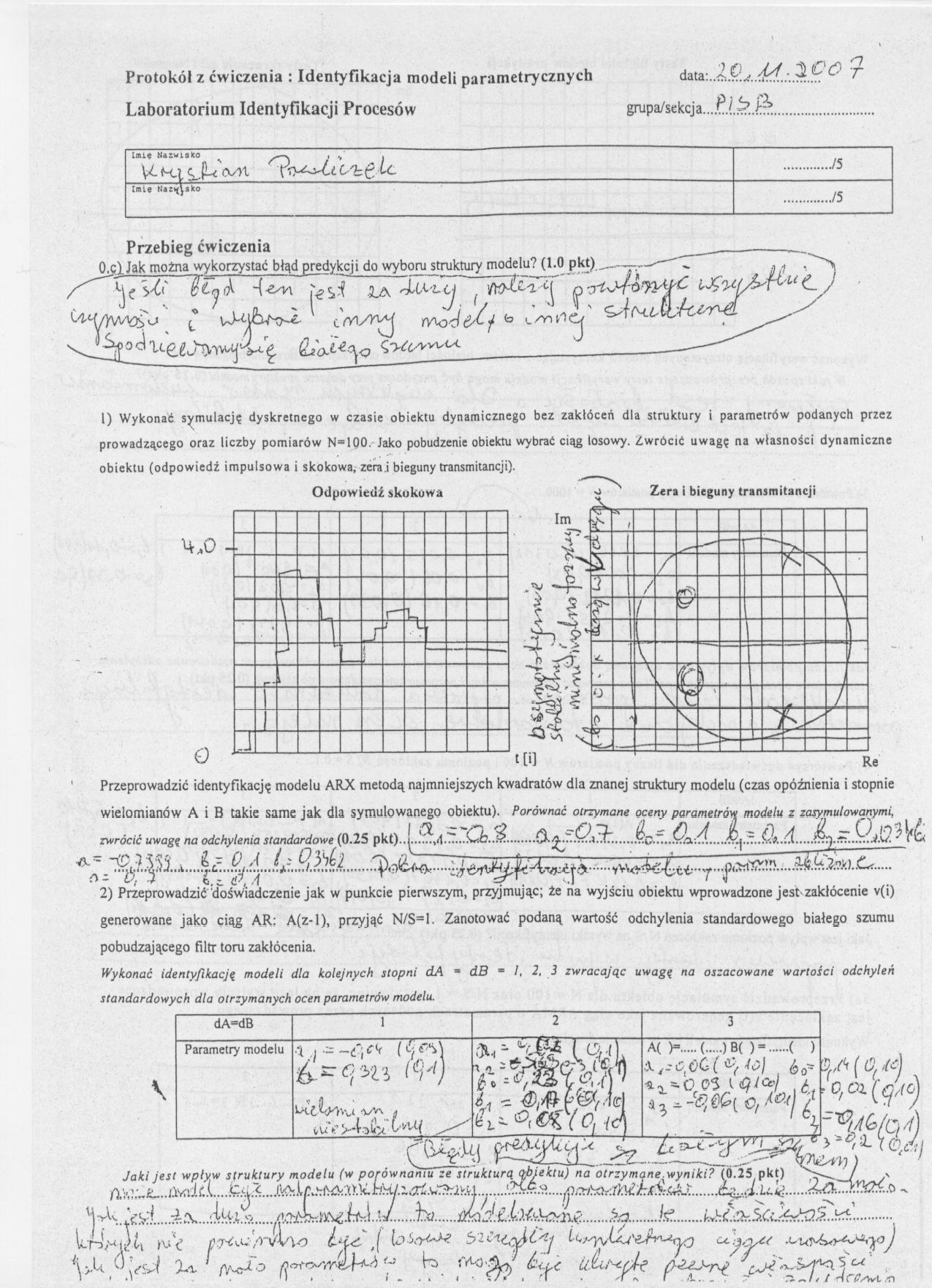
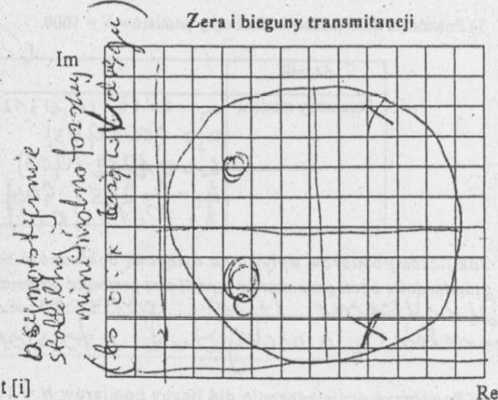
1) Wykonać symulację dyskretnego w czasie obiektu dynamicznego bez zakłóceń dla struktury i parametrów podanych przez prowadzącego oraz liczby pomiarów N=100. Jako pobudzenie obiektu wybrać ciąg losowy. Zwrócić uwagę na własności dynamiczne obiektu (odpowiedź impulsowa i skokowa, zera.i bieguny transmitancji).

Odpowiedź skokowa

u,o

		r-t
	l
		1				r	V,
		L			r	i
	-	T
	r*^1

o

' Przeprowadzić identyfikację modelu ARX metodą najmniejszych kwadratów dla znanej struktury modelu (czas opóźnienia i stopnie wielomianów A i B takie same jak dla symulowanego obiektu). Porównać Otrzymane oceny parametrów modelu z zasymulowanymi, zwrócić uwagę na odchylenia standardowe (0.25 pkt)..Cii?..s£..............^ę.~..triL.ul. ~ . ~..Q>..d. •' Vb<

......

2) Przeprowadzić doświadczenie jak w punkcie pierwszym, przyjmując; że na wyjściu obiektu wprowadzone jest zakłócenie v(i) generowane jako ciąg AR: A(z-l), przyjąć N/S=l. Zanotować podaną wartość odchylenia standardowego białego szumu pobudzającego filtr toru zakłócenia.

Wykonać identyfikację modeli dla kolejnych stopni dA ^m dB ^m I. 2, 3 zwracając uwagę na oszacowane wartości odchyleń standardowych dla otrzymanych ocen parametrów modelu.