Image30

58

Prędkość

v_x = x = l ę₀ co sincot sin(cp_a coscot),

v

y — — l cp_Q co sincot cos(cp₀ coscot),

v = l cp_a co sincot.

Przyspieszenie

v

a

n

l

= l cp_Q co^{1 2} sin²cot_y

a.

v

l cp co² cos cot,

a

= l cp_Q co² yjcos²cot 4- cp₀ sin⁴cot

1.24

a) a_c

= 2v x co,

a_c = 2v co sin cp

2 - co sintp

t

1

b) x = - a_c t² = stco sin cp,

JŁś

/V

3,6 • 10“² [m].

1.25. Zauważmy, że wektor prędkości kątowej Ziemi co tworzy z kierunki©

71

pionu kąt - — cp. Przyjmując prostokątny układ współrzędnych, którego oś x

skierowana jest z zachodu na wschód, zaś oś z pionowo w dół otrzymujemy:

#•

x = 2 vco cos cp = 2 cogt cos cp_y

2 = g.

Całkując te równania metodą rozdzielenia zmiennych, przy warunkach początkowych:

x (0) = x (0) — 0

oraz

2(0) = z(0)

0,

mamy

x =

1 ₃

- cogt³ cos cp,

Eliminując z tych równań czas, dostajemy

2 z

/V/

x — -

2

2 COZ COS (p

2,75 • 10 ² [m]

1.26. Wprowadzamy współrzędne sferyczne (rys. 16)

z = r cos#.

x = r sim9 cos(p,

y = r sin# sin<p,

9 = 9(t).

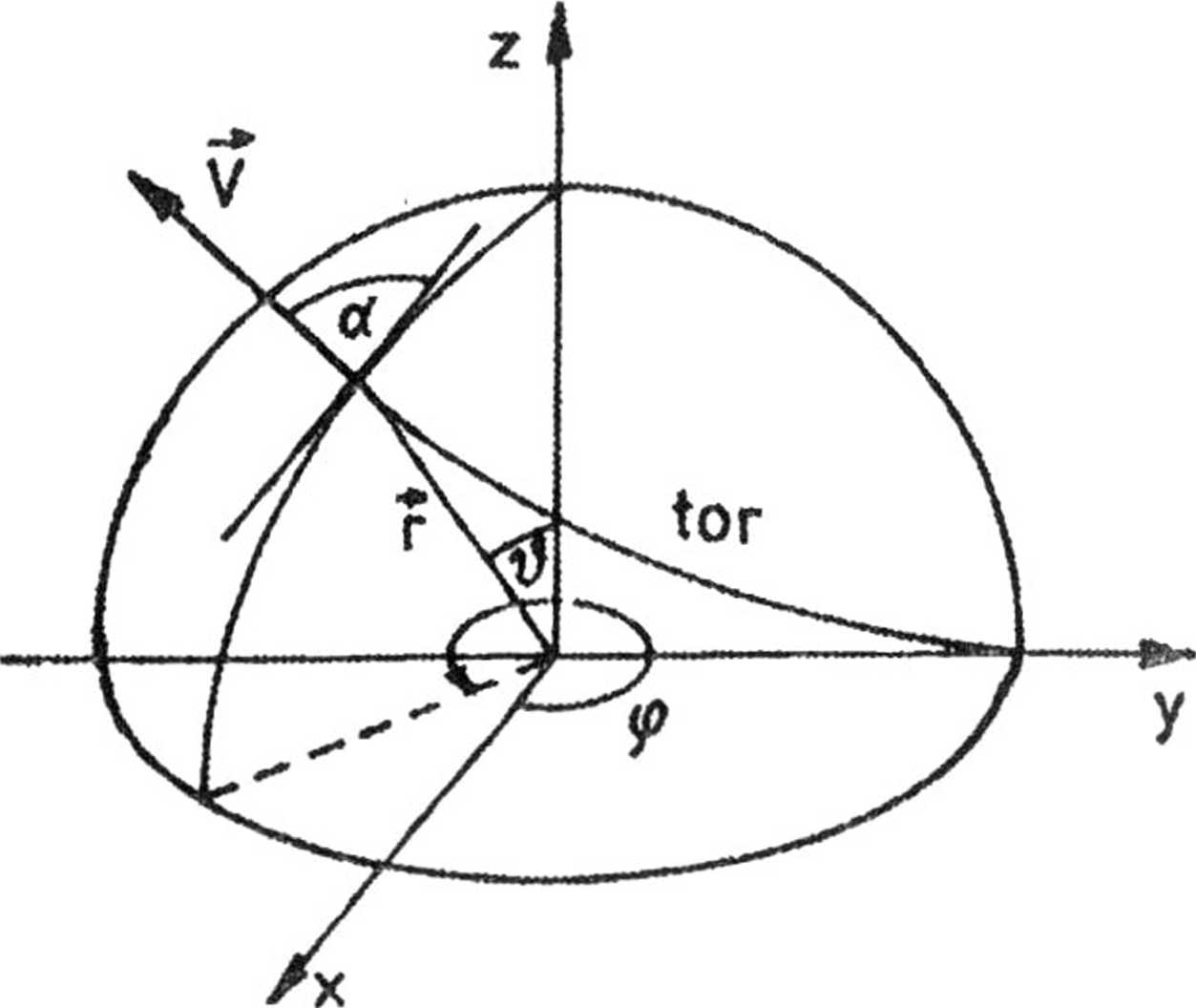
Rys. 16

Wtedy ruch punktu w przestrzeni w dowolnej chwili t określić możemy za pomocą trzech równań:

r = r(t),    _ (p = ę(t),

Wektor prędkości v rozkładamy na trzy składowe v_r,    o współrzędnych:

v_r = v_x cos (p sin# + v sin cp sin .9 -f

-f cos# = r,

v

<p

—    v_x sin<p 4- v_y coscp = r(p sin#,

— v_x co s(p cos # — v_y sin cp cos#

—    v„ sin# = r#.

Z warunków zadania wynika, że

v_r = 0,

v_<p = P<p sin#,

= -R9,

v

v

<p

ctga.

Stąd

dt

-R

d(p

R — sin# ctga. dt

Po rozdzieleniu zmiennych i przecałkowaniu mamy ostatecznie:

#

tg - = e'”'¹⁸*

1

2

= 2 ^9t