Image57 (10)

112

112

W naszy

(p = O, o = 0,4, co²

Stąd otrzymuje

przypadku

2,62 [s“²] i C =

6,7 • 1(T²

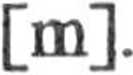
II

y równanie ruchu punktu

x + 0,8 x + 2,62 x = O

i jego rozwiązanie

6,7 • 10"² e

0,4t

n

b. Z warunku sin - t = sinco, t

2 ¹

0 znajdujemy czasy, w których punkt

znajduje się w położeniu równowagi w rozważanym przedziale [0, 27]

t

0,

t₂ — 2 [s],

*3 = 4 [s],

U = ⁶ C^s]»

= 8 [s].

Z warunku

0 znajdujemy czas = 0,84 [s], odpowiadający

pierwszemu maksimum lokalnemu funkcji x(t). Znając okres, znajdujemy stąd czasy odpowiadające kolejnym ekstremom lokalnym w rozważanym przedziale

[0, 27]

t'₂ = 2,84 [s],

f

4,84 [s],

= 6,84 [s]

Podstawiając znalezione wartości t! do równania ruchu otrzymujemy od powiadające im wartości wychylenia punktu. Na tej podstawie możemy sporzą dzić szukany wykres zależności x(t).

2.58. Równanie drgań kulki w cieczy ma postać

6nr]r .    -

x -f - x -f co x = 0,

m

gdzie x jest wychyleniem mierzonym względem położenia równowagi statycznej, t] jest współczynnikiem lepkości cieczy. Z teorii wiemy, że stały współczynnik

występujący przy prędkości ruchu jest równy podwójnemu współczynnikowi tłumienia drgań <r, a ten wiąże się z częstością drgań związkiem

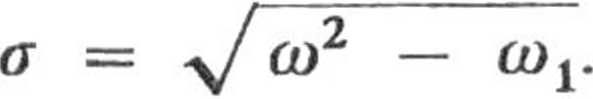
stąd

4

9

pr

y/ CO² —

CO

10 [kgm *s *]

2.59.

a)

d²x

dt²

+

ln2 dx

5 dt

-f 4n²x — 0.

b)    T = 1,006 [s].

c)    1,1 [W].

2.60. Równania ruchów drgających zapisujemy w postaci:

= x_a sin (co_xt + a),

x_a sin (co₂t + a).

Stąd ruch wypadkowy

co, + co₇

t sm I —— -- t + a

2

x = x, + x₀ =

2x_n cos ---

⁰ 2

przedstawia drganie harmoniczne, którego amplituda

A

t

_    (O i    (O 2

2a cos ---

2

zmienia się okresowo z częstością (co^ — co₂). Wobec tego okres dudnień

T =

2n

TJ

C0₁    ~ CO ₂

To

93 [s]

2.61. Przyjmując kartezjański układ współrzędnych, możemy zapisać rów nania drgań w postaci