Image58 (10)

2

(Ot +

y = A sincot.

Stąd równanie toru

x² + y²

przedstawia okrąg o promieniu ^4 = 0,05 [m].

2.62. Z kierunkami drgań wiążemy prostokątny układ współrzędnych, przyjmując początek układu w położeniu równowagi. Wobec tego równania drgań mają postać

x = A_l sincot, y — A₂ sincot.

Stąd równanie toru

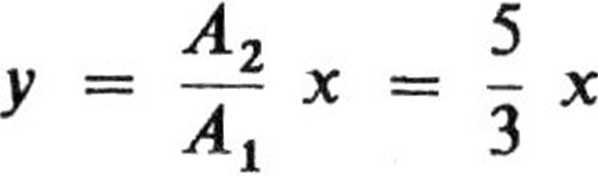
przedstawia prostą przechodzącą przez początek układu. Takie drgania nazywamy liniowo spolaryzowanymi.

2.63. Ruch wypadkowy jest opisany równaniem x — x_t + x₂ = A_v cos (cot + aj + A₂ cos (cot + a₂) =

= (At cosaj A A₂ cosa₂) coscot

(A_t sina₁ + ^4₂ sina₂) sincot

gdzie A_if a_lt A₂, a₂ oznaczają odpowiednio amplitudy i fazy ruchów składowych. Równanie ruchu zapiszemy w prostszej postaci, jeśli zauważymy, że zawsze można znaleźć takie dwie stałe A i a, że spełnione będą związki:

A₁ cosaj + A₂ cosa₂ = A cosa,

A sina,

A_t sinaj -f A₂ sina₂

A =    * 4- 2A_x A₂ cos (a₂ — a*) + A\,

czyli

a

arctg

/ii sinaj -f- A₂ sina₂ /li cosaj -f A₂ cosa₂

Po wstawieniu do równania ruchu otrzymujemy

x = A sin (cot + a),

gdzie A = 0,07 [m] jest amplitudą ruchu wypadkowego

2.64. Korzystając z wyniku zadania 2.60 mamy

1

T

40 [s'¹]

2.65. Różnica faz

A(p = 2n

l

n

X

10

gdzie /j i l₂ są odległościami zadanych punktów od źródła drgań.

2.66. Różnica faz Acp = 4n.

0,48 [m].

2.67. Długość fali X

2.68.    Promień fali załamanej będzie tworzył z powierzchnią wody kąt p = 40°ir.

2.69.    Odległość między węzłami fali stojącej

(2 n + 1)

= 0, 1, 2, 3,

gdzie: n Stąd

v = Xv = 1425 [ms *].