img016 (46)

21

21

(2.24)

^aV '■= 4/V^akk ^dla j = k,k +1, ■ • •, n,

H 8t; « remie o numerze k otrzymane w punkcie a) jest mnożone kolejno przez współczyn-( mk — a\l¹, i = k +1, k + 2, ■ ■ ■, n , i dodawane stronami do równania o numerze i otrzymanego w poprzednim kroku:

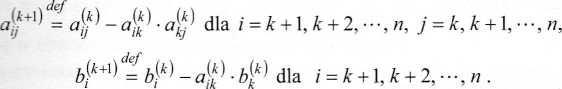
(2.25)

(2.26)

W kroku n równanie o numerze 77 jest dzielone przez aft * rcocedurze napisanej dla komputera należy podstawić za aft^+l * dla i = k + 1, k + 2, • • •,

ł a irtość dokładną zero, aby uniknąć wpisania pewnych małych i różnych od zera liczb. Zr c' należy przyjąć wartość dokładną jeden.

W wyniku otrzymuje się równoważny danemu układ równań liniowych postaci

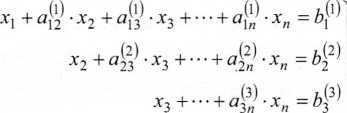
(2.27)

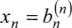
Współczynniki i składowe wektora wyrazów wolnych w układzie równań (2.27) różnią się od odpowiednich współczynników i składowych wektora wyrazów wolnych o tych samych indeksach w wyprowadzonym poprzednio układzie równań (2.16) równoważnym układowi (2.27). Współczynniki i składowa wektora wyrazów wolnych w równaniu o numerze i, i= 1,2, •••,«, układu równań (2.27) są równe współczynnikom i składowej wektora wyrazów wolnych w równaniu o tym samym numerze w układzie równań (2.16), po podzieleniu tych ostatnich przez aft.

W metodzie dekompozycji LU (podrozdział 2.2.) będą wykorzystywane obie wersje otrzymywanego w etapie eliminacji w przód układu trójkątnego górnego. Będzie też zawsze wyraźnie zaznaczone, który z układów jest przedmiotem rozważań.

Wzór obliczeniowy na wyznaczanie współrzędnych wektora rozwiązania danego układu równań w etapie podstawiania wstecz

Jeżeli w obliczeniach z wykorzystaniem komputera korzysta się z postaci (2.27) układu równań przekształconego w etapie eliminacji w przód, to składowe x_t, i = 1, 2, n, wektora rozwiązania otrzymuje się ze wzoru