Wydział Metali Nieżelaznych 7 XI 2005

Metalurgia

Rok II

ZESPÓŁ 5

Ćwiczenie nr. 2

Napięcie powierzchniowe w układzie

faza ciekła ­ - faza gazowa

Owcarz Joanna

Wstęp:

Cząstka cieczy, znajdująca się na powierzchni fazowej ciecz-gaz, jest poddana oddziaływaniu sił między powierzchniowe obydwu ośrodków. Siła wypadkowa, skierowana prostopadle do powierzchni fazowej, dąży, do wciągnięcia cząstki w głąb cieczy. Objawia się to dążnością układu do zmniejszenia powierzchni fazowej. Zjawisko to nazywa się napięciem powierzchniowymi Miarą napięcia powierzchniowemu jest siła działająca na jednostkę długości na powierzchni fazowej ( siła styczna do tej powierzchni, dążąca do jej Zmniejszenia) lub praca potrzebna do zwiększenia powierzchni fazowej o jednostkę. Równoważnymi wymiarami napięcia powierzchniowemu są więc
oraz
.

Najmniejszą wartość stosunku wielkości powierzchni do objętością wykazuje kula. W wyniku działania napięcia powierzchniowemu dążącego do zmniejszenia powierzchni fazowej, ciecze zawieszone w fazie gazowej przyjmują kształt kulistych kropel itp. krople mgły. Zjawisko to staje się bardziej złożone w przypadku zetknięcia się trzech faz, itp. dwie fazy ciekłe i faza gazowa lub fazy ciekła, stała i gazowa itp. Na cząsteczkę cieczy znajdującą się na granicy zetknięcia się trzech faz oddziaływają siły międzycząsteczkowe trzech, ośrodków. W zależności od tego czy napięcia powierzchniowego na granicy faz ciekła-gazowa jest mniejsze czy większe niż na granicy faz ciekła-stała brak zwilżalności lub zwilżanie. . W obydwu przypadkach (powierzchni lub brak zwilżalności) zwiększa się ta powierzchnia, której rozbudowa jest związana z mniejszym nakładem energii.

Tematem ćwiczenia jest napięcie powierzchniowe na granicy faz ciekłej i gazowej. Napięcie powierzchniowe właściwe wyznacza się w układzie nie zawierającym obcych gazów (ciecz-para). powierzc obcych gazów, gdy nie reagują one z badaną cieczą, wpływa w powierzchniow małym stopniu na mierzoną wielkość.

Zależność napięcia powierzchniowemu cieczy od temperatury opisuje wyprowadzone przez Etövösa równanie (1):

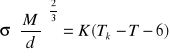
(1)

gdzie: M oznacza ciężar cząsteczkowy, d - ciężar właściwy (stąd
jest objętością jednego mola), T_K - temperatura krytyczna, K jest wartością stałą (w przypadku cieczy organicznych wynosi ona 2,12.).

Zależność napięcia powierzchniowemu od stężenia substancji rozpuszczonych posiada charakter złożony, zależny od rodzaju układu. Dla wodnych powierzch kwasów powierzchnio zależność tę ujmuje wyprowadzone przez Szyszkowskiego równanie (2):

(2)

gdzie:
oznacza napięcie powierzchniowe czystego rozpuszczalnika,
- roztworu, a oraz b są stałymi, c - stężeniem. Zależność napięcia powierzchniowemu od stężenia wiąże się w tym przypadku ze powierzchn adsorpcji substancji rozpuszczonej na granicy fazowej. Gdy mówimy o stopach metali brak jest ogólnego równania powierzchn zależność napięcia powierzchniowemu od stężenia, a dodatkowym czynnikiem komplikującym sytuację w tych układach jest powierzch powstawania różnych związków.

Z definicji napięcia powierzchniowego wiemy że, zmiana wielkości powierzchni fazowej wiąże się z efektami energetycznymi. Zmiana energii swobodnej związana ze wzrostem powierzchni o 1 cm² jest równa potrzebnej do tego pracy, stąd możemy wnioskować, że energia swobodna 1 cm² powierzchni fazowej jest równa napięciu powierzchniowemu:

(3)

Gdy uwzględnimy znane zależności :

i

możemy przedstawić U, czyli całkowita energię 1 cm² powierzchni fazowej w postaci:

(4)

II Metody pomiarowe.

Pierwszą metodą jest metoda stalagmometryczna, polegająca na pomiarze ilości kropel powstających podczas wypływu określonej objętości cieczy z rurki kapilarnej. Krople odrywają się od rurki w momencie gdy ich ciężar przewyższy działającą na obwodzie przewężenia kropli, siłę napięcia powierzchniowego równą
. Tak więc powstające krople są tym większe (tym mniej ich powstaje z określonej objętości), im większe jest napięcie powierzchniowe. Stosunek napięć powierzchniowych dwóch cieczy można wyliczyć ze wzoru:

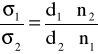
gdzie: d i n - odpowiednio ciężary właściwe i liczby kropel badanych cieczy.

Drugą metodą jest metoda pęcherzykowa, polegająca na pomiarze ciśnienia, potrzebnego do wypchnięcia pęcherzyka gazu, poprzez rurkę kapilarną do badanej cieczy. Ciśnienie to mierzy się zazwyczaj układem manometrycznym w postaci ururki, z której odczytuje się różnicę poziomów cieczy manometrycznej w momencie wypchnięcia pęcherzyka gazu. Stosunek napięć powierzchniowych dwóch cieczy można wyliczyć ze wzoru:

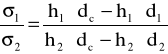
gdzie: h' - różnica poziomów cieczy manometrycznej, h - głębokość zanurzenia kapilary, d_c - ciężar właściwy cieczy manometrycznej, d₁ i d₂ - ciężary właściwe badanych cieczy

Cel ćwiczenia:

1. Pomiar napięcia powierzchniowego alkoholu oraz roztworu mydła metodami stalagnometryczną i pęcherzykową. Wyznaczenie błędów względnych i ocena dokładności metod.

2. Pomiar napięcia powierzchniowego (metodą stalagmometryczną lub pęcherzykową) roztworów alkoholu o różnych stężeniach. Ustalenie w oparciu o uzyskane wyniki zakresu stosowalności równania Szyszkowskiego oraz ewentualne wyznaczenie współczynników tego równania.

3. Wykreślenie na podstawie danych tabelarycznych zależności napięcia powierzchniowego wody, glinu, cynku, cyny, ołowiu i miedzi od temperatury. W oparciu o ten wykres należy wyznaczyć wartości
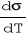
   . Należy również wyznaczyć całkowitą energię powierzchniową tych substancji (równie (4)).

Wyniki pomiarów

1.

	Metoda stalagmometryczna				Metoda pęcherzykowa
Substancja	Ilość kropel w kolejnych pomiarach n	Ciężar właściwy d			Manometryczna różnica poziomów h'	Głębokość zanurzenia kapilary h
	-		-				-
H2O	48	1.00	1.00	72.583	31	21	1.00	72.583
					49							28
					47							28
					48							29
	alkohol 100%				143				0.807	0,266	19,307	18	21	0,298	21,630
					150							20
					144							20
					145,67							19,33
	0.1% roztwór mydła				76				1.00	0,634	46,017	27	21	0,834	60,534
					75							28
					76							28
					75,67							27,67

1.Obliczenia dla metody stalagmometrycznej

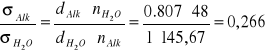
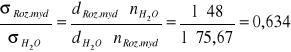
2.Obliczenia dla metody pęcherzykowej:

d_m=1

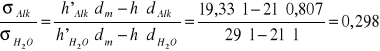
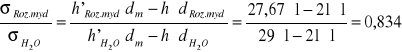
3.Obliczanie błędu względnego dla metody stalagmometrycznej:

Rzeczywisty ciężar właściwy wody: 0,9982[g/cm³]

Przyjęty w obliczeniach ciężar właściwy wody: 1[g/cm³]


=1-
=1- 0,9982=0,0018[g/cm³]≈ 0,002[g/cm³]

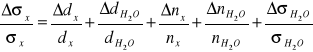
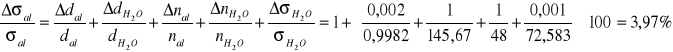
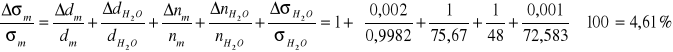
i pęcherzykową:

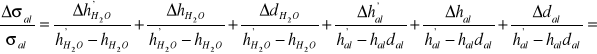
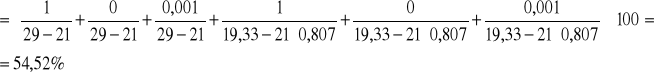
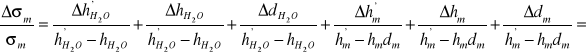
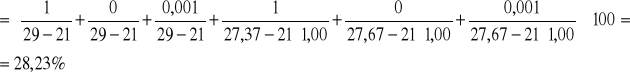
4. Wyniki pomiarów napięcia powierzchniowego roztworów wodnych alkoholu o różnych stężeniach.

Metoda stalagmometryczna:

Sporządzanie roztworów	Stę- żenie [%]	Ciężar właściwy dX [g/cm^3]	Ilość kropel nX [mm]	Napęcie powie-rzchniowe σ [dyn/cm]	Błąd wzgl. [%]
Roztwór wodny alkoholu metylowego	100	0,807	143 150 144 śr.:145,67	19,307	3,97	-0,193	-5,18
20ml roztw.100% + 5ml H2O	80	0,859	144 144 142 śr.: 143,33	20,904	3,98	-0,261	-3,83
25ml roztw.80% + 8,3ml H2O	60	0,909	142 140 141 śr.:141	22,501	3,99	-0,375	-2,67
33,3ml roztw.60% + 16,7ml H2O	40	0,948	136 136 136 śr.:136	24,315	4,02	-0,608	-1,65
20ml roztw.40% + 20ml H2O	20	0,974	102 103 102 śr.:102,33	33,170	4,26	-1,659	-0,60
20ml roztw.20% + 20ml H2O	10	0,985	80 74 79 śr.:77,67	44,203	4,57	-4,420	-0,23
20ml roztw.10% + 20ml H2O	5	0,991	64 64 64 śr.:64	53,947	4,85	-10,789	-0,09
10ml roztw.5% + 40ml H2O	1	0,997	54 58 60 śr.:57,33	60,607	5,03	-60,607	-0,02

Metoda pęcherzykowa:

Sporządzanie roztworów	Stę- żenie [%]	Ciężar właściwy dX [g/cm^3]	Ciśnienie mano-metryczne h'X [mm]	Głębokośc zanurzenia kapilary hX [mm]	Napęcie powie-rzchniowe σ [dyn/cm]	Błąd wzgl. [%]
Roztwór wodny alkoholu metylowego	100	0,807	18 20 20 śr.:19,33	21	21,630	54,52	-0,216	-4,62
20ml roztw.100% + 5ml H2O	80	0,859	15 20 20 śr.:18,33	21	2,64	356,50	-0,033	-30,30
25ml roztw.80% + 8,3ml H2O	60	0,909	20 20 20 śr.:20	21	8,265	122,39	-0,138	-7,26
33,3ml roztw.60% + 16,7ml H2O	40	0,948	22 22 22 śr.:22	21	18,980	60,36	-0,475	-2,11
20ml roztw.40% + 20ml H2O	20	0,974	23 33 21 śr.:25,67	21	47,324	31,70	-2,366	-0,42
20ml roztw.20% + 20ml H2O	10	0,985	27 23 27 śr.:25,67	21	45,228	32,59	-4,523	-0,22
20ml roztw.10% + 20ml H2O	5	0,991	27 25 25 śr.:25,67	21	44,085	33,11	-8,817	-0,11
10ml roztw.5% + 40ml H2O	1	0,997	26 25 25 śr.:25,67	21	42,942	33,66	-42,942	-0,02

5. Zależność napięcia powierzchniowego szeregu metali od temperatury.

H2O			Al			Cu				Zn			Sn				Pb
t	σ	Ui	t	σ	Ui	t	σ	Ui	t		σ	Ui		t	σ	Ui	t	σ	Ui
[^oC]			[^oC]		]	[^oC]			[^oC]		]			[^oC]			[^oC]
0	75,626	75,626	706	494	593,5	1131	1103	416,5	420		773,0	855,9		232	578,8	624,9	327	469,9	524,1
5	74,860	75,695	762,2	489	596,5	1150	1145	447,0	505		762,2	861,8		250	575,8	625,5	370	465,9	527,2
10	74,113	75,783	794	483	595,0	1200	1154	425,6	545		749,5	857,0		300	566,0	625,6	425	447,3	517,8
15	73,350	75,855	816	480	595,1	1215	1166	428,5	616		739,7	861,2		350	556,2	625,8	472	443,4	521,7
20	72,583	75,923	897	469	595,5				635		728,9	854,2		400	545,4	624,9	507	440,5	524,6
25	71,810	75,985	906	466	593,7									450	535,6	625,1	557	430,7	523,1
30	71,035	76,045	935	463	594,8									500	525,8	625,2	610	421,8	522,9
35	70,230	76,075												550	516,0	625,3	657	415,9	524,8
40	69,416	76,096												600	506,2	625,5
45	68,592	76,107
50	67,799	76,149
55	66,894	76,079
60	66,040	76,060
65	65,167	76,022
70	64,274	75,964
75	63,393	75,918
80	62,500	75,860
85	61,587	75,782
90	60,684	75,714
95	59,763	75,628
Wartość średnia U		75,918			594,9			429,4				858,0				75,918			625,3

• H­₂O

• Al

• Cu

• Zn

• Sn

• Pb

Wnioski:

Metoda stalagmometryczna jest metodą dokładniejsza od metody pęcherzykowej. Błędy względne metody stalagmometrycznej wyniosły kilka, a metody pęcherzykowej kilkadziesiąt , a nawet kilkaset procent. Tak duży błąd dla metody pęcherzykowej jest wynikiem odczytu różnicy poziomów cieczy manometrycznej z dokładnością do 1mm, a różnica ta wynosiła od kilku do kilkunastu mm, co daje bardzo duży błąd.

Równanie Szyszkowskiego jest spełnione dla obu metod pomiarowych.

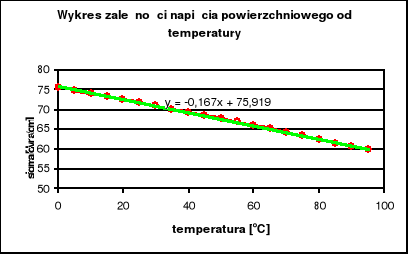
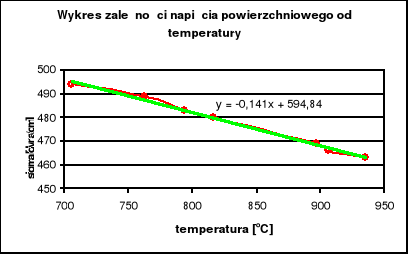
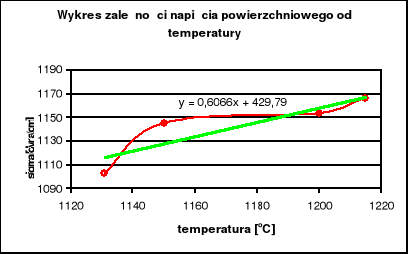
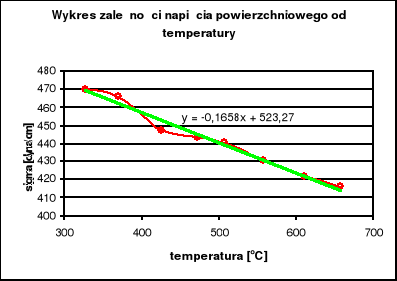
Punkty (zależności napięć powierzchniowych metali od temperatury) układają się wzdłuż linii prostych, za wyjątkiem miedzi. Kąty nachylenia tych prostych pozwalają nam na wyliczenie energii 1cm² powierzchni fazowej metali.

11

Z wykresu odczytuję równanie prostej:

y = -0,167⋅x + 75,919

σ = -0,167⋅t + 75,919

-0,167

Całkowita energia 1cm² powierzchni fazowej wynosi:

U_i = σ - t⋅

U =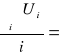
75,918

Z wykresu odczytuję równanie prostej:

y = -0,141⋅x + 594,84

σ = -0,141⋅t + 594,84

-0,141

Całkowita energia 1cm² powierzchni fazowej wynosi:

U_i = σ - t⋅

U =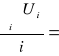
594,84

Z wykresu odczytuję równanie prostej:

y = -0,6066⋅x + 429,79

σ = -0,6066⋅t + 429,79

-0,6066

Całkowita energia 1cm² powierzchni fazowej wynosi:

U_i = σ - t⋅

U =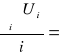
429,79

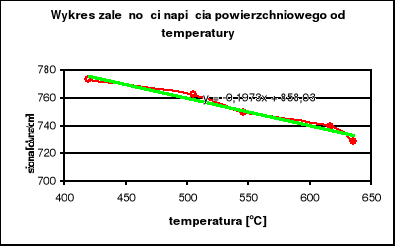
Z wykresu odczytuję równanie prostej:

y = -0,1973⋅x + 858,03

σ = -0,1973⋅t + 858,03

-0,1973

Całkowita energia 1cm² powierzchni fazowej wynosi:

U_i = σ - t⋅

U =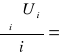
858,03

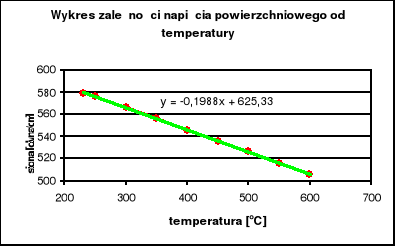
Z wykresu odczytuję równanie prostej:

y = -0,1988⋅x + 625,33

σ = -0,1988⋅t + 625,33

-0,1988

Całkowita energia 1cm² powierzchni fazowej wynosi:

U_i = σ - t⋅

U =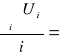
625,33

Z wykresu odczytuję równanie prostej:

y = -0,1658⋅x + 523,27

σ = -0,1658⋅t + 523,27

-0,1658

Całkowita energia 1cm² powierzchni fazowej wynosi:

U_i = σ - t⋅

U =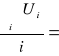
523,27

---