Ćwiczenie 15

Wyznaczanie prędkości dźwięku w powietrzu i ciałach stałych.

Wstęp:

Pojęcie fali.

Przez falę w ośrodku stałym, ciekłym czy gazowym rozumiemy rozchodzenie się zaburzeń (zakłócenie stanu równowagi) ośrodka wywołanych lokalnie. Rozchodzeniu się zaburzeń w ośrodku towarzyszy transport energii. Lokalne zmiany stanu ośrodka wywołane źródłem fali rozprzestrzeniają się ze skończona prędkością. Jeśli źródło fali wywołuje ruch harmoniczny cząstek ośrodka, mówimy o fali harmonicznej. Równanie fali harmonicznej ma postać:

(1)

gdzie: A - amplituda wychylenia cząsteczek ośrodka,

- częstość kołowa,

T - okres drgań cząstek ośrodka [s],

ν - częstość [1/s],

v - prędkość rozprzestrzeniania się fali [m/s].

Graficznym przedstawieniem równania fali zarówno w funkcji czasu t przy ustalonym x, jak i funkcji x przy ustalonej chwili t jest sinusoida jak na rys.1. powyższe równanie fali dotyczy fali płaskiej (w równaniu występuje tylko jedna współrzędna miejsca - x) co oznacza, że czoło fali przemieszcza się w dodatnim kierunku osi ox dla znaku - i ujemnym dla znaku +. Dla zadanej wartości x, np. x = x₁ wychylenia wszystkich punktów są takie same. Mówimy wówczas , że płaszczyzna x = x₁ jest płaszczyzną stałej fazy ruchu (czoło fali), przez fazę zaś rozumiemy argument funkcji cos, tj:
.

Rys.1. Ilustracja równania fali

Interferencja fal.

Jeżeli w ośrodku rozchodzi się kilka fal, które np. rozprzestrzeniają się wzdłuż osi ox, to fale te oddziaływują ze sobą w złożony sposób. Gdy źródło każdej z fal wytwarza falę w krótkim przedziale czasu i gdy czasy rozpoczęcia emisji fal są przypadkowe, wówczas otrzymany ciąg fal jest niespójny i mówimy, że mamy do czynienia z superpozycją fal. Przykład niespójnego ciągu fal przedstawiono na rys.2. Niespójność polega na tym, że przy złożeniu poszczególnych fal występują skokowe, różne zmiany fazy, np. pomiędzy 1 i2 jest ¼Tω, zaś pomiędzy 2 i 3 jest ½Tω. Jeśli przesunięcia w fazie dla wszystkich fal są takie same, to ciąg fal nazywamy spójnym. Oddziaływanie fal niespójnych nazywamy superpozycją fal, (jej wynik jest złożony) natomiast oddziaływanie fal spójnych nazywamy interferencją ( jej wynik da się opisać w sposób przejrzysty).

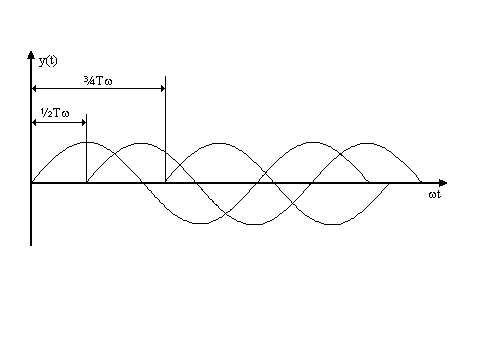
Rys.2. Ciąg fal niespójnych

Fale stojące

Weźmy pod uwagę dwie fale płaskie biegnące w przeciwnych kierunkach. Równania tych fal mają postać:

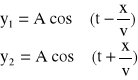
(2)

Amplitudy obu fal są takie same (A), takie same są również częstotliwości kołowe drgań (ω). Złożenie obu fal, poprzez zastosowanie wzorów trygonometrycznych, daje wyrażenie:

(3)

Pierwszy człon tego równania opisuje amplitudę fali. Amplituda ma wartość zerową (w każdej chwili czasu t) jeśli:
n=1,2,3,... Oznacza to, że w miejscach
cząstki ośrodka znajdują się w spoczynku. Miejsca te nazywamy węzłami fali. Amplituda zaś jest maksymalna, gdy:
, co zachodzi dla
. Miejsca maksymalnej amplitudy nazywamy strzałkami (rys.3).

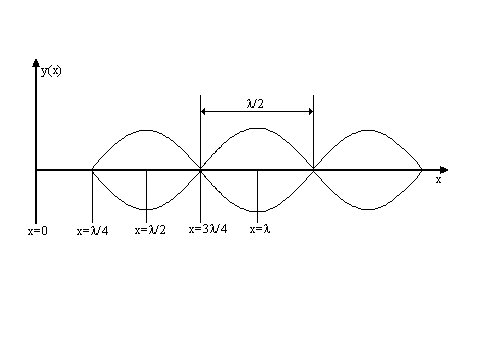
Rys.4. Fala stojąca

Fala stojąca może powstać jeśli fala padająca ulega odbiciu i fala odbita interferuje z falą padającą. Odbicie fali od ośrodka gęstszego następuje ze zmianą fazy o π (strata ½ długości fali), zaś odbicie od ośrodka rzadszego następuje bez zmiany fazy.

Przebieg ćwiczenia:

1. Przyrządy:

Układ Quinckiego, rura Kundta, pręty metalowe, kalafonia;

Do pomiaru prędkości dźwięku w różnych ośrodkach wykorzystuje się metodę rezonansu. Rezonans ma miejsce wtedy, gdy częstotliwość drgań źródła wzbudzającego drgania pokrywa się jedną z częstotliwości drgań własnych wzbudzanego układu.

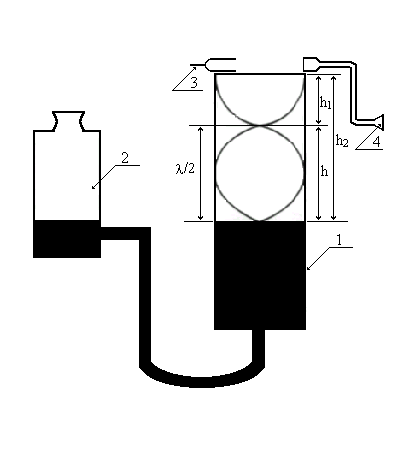
Do wyznaczenia prędkości fali dźwiękowej w powietrzu zastosowano układ Quinckiego (rys.4). Wykorzystano tutaj zjawisko rezonansu akustycznego między drgającym kamertonem (3), a drganiami słupa powietrza nad wodą w rurze (1).

Rys.4. Układ Quinckiego

Należy zmierzyć odległość h pomiędzy dwoma położeniami poziomu cieczy, dla których słychać w słuchawce (4) wzmocnienia dźwięku. Jeśli są to wzmocnienia następujące kolejno po sobie to:
, a stąd:
.

Prędkość dźwięku wyznaczyć można ze wzoru:

(4)

gdzie: ν_k - częstość drgań własnych kamertonu.

Do wyznaczenia prędkości fali w prętach wykorzystano rurę Kundta (rys.5). W rurze Kundta wykorzystuje się rezonans między drganiami podłużnymi w pręcie (1) wykonanym z badanego materiału i drganiami słupa powietrza w rurze (2) ograniczonego płytką na końcu badanego pręta i zakończeniem przysłony (3).

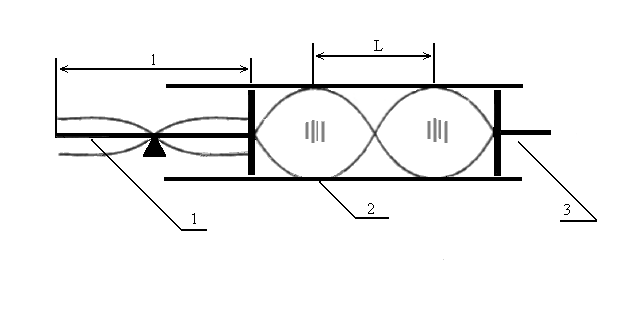
Rys.5. Rura Kundta

Jeśli oznaczymy przez λ₁ i v₁ oraz λ i v długość i prędkość fali odpowiednio w pręcie i powietrzu, to dla rezonansu zachodzi związek:

(5)

Długość fali w powietrzu i pręcie wyznaczamy odpowiednio z zależności:
gdzie n - jest ilością połówek fali stojącej w słupie powietrza o długości L (rys.5), zaś l - długością badanego pręta.

Prędkość fali v₁ wyznaczamy na podstawie zależności:

(6)

Prędkość ta jest zależna od gęstości badanego materiału oraz modułu Younga, co pokazuje poniższy wzór:

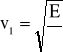
(7)

2. Pomiary i obliczenia:

1. Wyznaczyć prędkość fali dźwiękowej metodą Quinckiego (patrz rys.4):

1. Obniżyć poziom wody w rurze (1) opuszczając pojemnik (2)

2. Wzbudzić kamerton (3) do drgań i umieścić go nad rurą (1)

3. Podnosić poziom cieczy w rurze nasłuchując w słuchawce (4) wzmocnienia dźwięku, zaznaczyć kredą poziom cieczy w chwili jego wzmocnienia.

4. Zanotować w tab.1 położenia h₁ i h₂ dla przynajmniej dwóch rezonansów w rurze

5. Ocenić błędy pomiarów Δh₁ = Δ h₂ = Δ h

Tab.1.

h1 [m]	h2 [m]	νk [Hz]	h [m]	v [m/s]	Δv [m/s]

2. Wyznaczyć prędkość dźwięku w prętach z badanych materiałów (patrz rys.5):

1. Umocować badany pręt (1) w środku jego długości wsuwając go do rury z wysypanymi opiłkami korka.

2. Wywołać podłużne drgania pręta za pomocą sukna posypanego kalafonią.

3. Podczas drgań pręta przesuwać tłoczek (3) tak, by powstał rezonans, który ujawni się powstaniem fali stojącej w rurze (jest to sygnalizowane charakterystycznym ułożeniem się opiłek korka).

4. Zmierzyć długość słupa powietrza L biorąc możliwie dużą liczbę połówek fali stojącej.

5. Zapisać wyniki do tab.2.

6. Powtórzyć pomiary jak w pkt. a) - d) dla prętów z różnych materiałów.

7. Ocenić błędy pomiaru Δl i ΔL.

Tab.2.

Nazwa pręta	l [m]	Δl [m]	L [m]	ΔL [m]	n -	v1 [m/s]	Δ v1 [m/s]	E [N/m^2]	ΔE [N/m^2]

3. Obliczyć prędkość dźwięku w powietrzu korzystając ze wzoru (4).

4. Obliczyć prędkość dźwięku w materiale wykorzystując wzór (6).

5. Obliczyć moduły Younga dla badanych materiałów przekształcając odpowiednio zależność (7).

6. Obliczyć maksymalne błędy bezwzględne Δv, Δv₁, ΔE odpowiednio wg wzorów (verte):

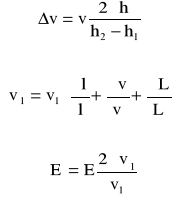
7. Wyniki należy zapisać w postaci: v= v_obl ± Δv , v₁= v_1obl ± Δv₁ , E= E_obl ± ΔE.

1

---