Ćwiczenie 72

Wyznaczanie współczynnika załamania światła za pomocą mikroskopu

Przyrządy:

Mikroskop z czujnikiem zegarowym, płytki płasko-równoległe z badanego materiału, śruba mikrometryczna.

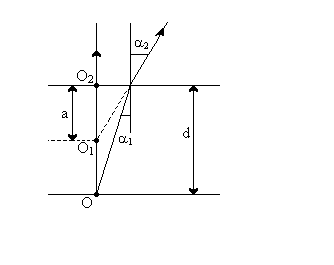
Oglądając punkt O przez warstwę materiału (rysunek obok), widzimy jego obraz O₁. Grubość pozorna płytki a, równa odległości O₁O₂, jest zależna od grubości rzeczywistej płytki d i jej współczynnika załamania n.

Dla ośrodka jednorodnego optycznie współczynnik załamania n jest równy:

(1)

Przy założeniu, że kąty α₁ i α₂ są małe, współczynnik załamania n dla rozważanej płytki wyrazi się wzorem:

(2)

Punkty O₁ i O₂ , a ściślej ostry obraz rys zaznaczonych na powierzchni płytki, obserwuje się przez mikroskop wyposażony w czujnik zegarowy, co pozwala na wyznaczenie grubości pozornej badanej płytki z odczytywanych położeń tubusu, odpowiadających położeniom ostrego obrazu rys.

Przebieg ćwiczenia:

1. Dokonać pomiaru grubości płytek d przy pomocy śruby mikrometrycznej.

2. Umieścić płytkę na stoliku mikroskopu i podnieść stolik mikroskopu tak, aby obiektyw znajdował się tuż nad powierzchnią płytki.

3. Patrząc w okular mikroskopu przesuwać powoli stolik w dół do chwili uzyskania ostrego obrazu dolnej powierzchni płytki.

Wyzerować wskazanie czujnika zegarowego.

4. Przesunąć stolik mikroskopu w dół tak, by uzyskać ostry obraz górnej powierzchni płytki. Odczytać wskazanie czujnika a.

5. Powtórzyć pięciokrotnie pomiary jak w pkt.3 i 4 rozregulowując za każdym razem ostrość obrazu.

Wyniki pomiarów zapisać w tab.1. Na ich podstawie obliczyć wartość średnią a oraz średni błąd kwadratowy S_a pojedynczego pomiaru, skorygowany przez odpowiedni współczynnik t_α,k (α - poziom ufności, k - ilość pomiarów): S_a= S_a t_α,k.

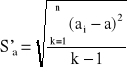
Tab.1.

a1 [mm]	a2 [mm]	a3 [mm]	a4 [mm]	a5 [mm]	a [mm]	S'a [mm]	tα, k	Sa [mm]

6. Wykonać jednokrotne pomiary grubości pozornej płytek odczytując wskazania a₁ i a₂ czujnika zegarowego otrzymane dla ostrego obrazu dolnej i górnej powierzchni płytek (nie zerować czujnika).

Pozorna grubość płytki jest wówczas równa różnicy wskazań:

a = |a₁ - a₂|

7. Obliczyć wartości współczynników załamania n dla badanych płytek ze wzoru (2) i wartości błędu Δn korzystając z poniższego wzoru (4):

(4)

8. Wyniki pomiarów i obliczeń zestawić w tab.2.

Tab.2.

Rodzaj płytki	d [mm]	Δd [mm]	a1 [mm]	Δa1 [mm]	a2 [mm]	Δa2 [mm]	n -	Δn -

Wymagania:

• Prawo odbicia i załamania światła na granicy ośrodków przeźroczystych.

• Wyprowadzenie wzorów (2) i (4).

• Wyjaśnienie pojęć i relacji: błąd średni kwadratowy, poziom ufności; błąd pomiaru, a błąd systematyczny i statystyczny.

• Zjawisko całkowitego wewnętrznego odbicia. Kąt graniczny - wyprowadzenie wzoru.

• Rozszczepienie światła białego - przejście światła przez pryzmat.

• Wyprowadzenie prawa załamania i odbicia na gruncie teorii falowej światła. Bezwzględny i względny współczynnik załamania światła. Wzór Newtona dla prawa załamania.

• Zależność współczynnika załamania od częstości padającego światła: uzasadnienie, ogólny charakter zależności, wyprowadzenie wzoru dla substancji bezpostaciowych.

2

---