1.Wstęp teoretyczny.

Prąd elektryczny jest to zjawisko fizyczne wywołane uporządkowanym ruchem ładunków elektrycznych przez badany przekrój poprzeczny danego ośrodka. Przepływ prądu elektrycznego wywołuje zjawiska: magnetyczne, cieplne, chemiczne, mechaniczne, świetlne i inne za pośrednictwem których poznaje się istnienie prądu elektrycznego.

Rozróżnia się m. inn. prąd elektryczny:

• stały - prąd jednokierunkowy , którego natężenie nie ulega zmianie w fumkcji czasu

• zmienny - w funkcji czasu zmienia się natężenie lub zwrot.

Jeśli w przypadku prądu zmiennego zmiany zachodzą okresowo , to prąd taki nazywa się przemiennym , a wartość średnia całookresowa natężenia pr\ądu równa się zeru.

i _śr (t) = (1/ T) ∫ i (t)dt = 0

gdzie: T - okres zmian prądu - czas , w którym prąd wykonuje jeden cykl zmian.

Najprostszym i najczęściej spotykanym prądem elektrycznym przemiennym jest prąd sinusoidalny, którego przebieg jest sinusoidalną funkcią czasu.

i(t) = Im sin(ωt + ϕ)

gdzie: i(t) - wartość chwilowa natężenia prądu.

I_m - wartość szczytowaprądu.

ω - pulsacja (częstość kątowa) ω = 2πf ; f - częstotliwość

ϕ - faza początkowa (początkowy kąt fazowy) - wielkość ta pozwala określić wartość prądu w chwili początkowej , tj. w chwili od której rozpoczęto rozpatrywać przwbieg danej wielkości.

Prąd przemienny charakteryzują również takiewielkości jak wartość średnia prądu oraz wartość skuteczna.

Wartość skuteczną określa poniższy wzór:

I_SK = √ (1/T) ∫ i² (t)dt

Interpretacja fizyczna wartości skutecznej prądu przemiennego jest następująca::

Wartość skuteczna natężenia prądu, jest to wartość liczbowo równa takiej wartości prądu stałego, który w tym samym czasie i na tym samym oporze wydzieli taką samą ilość ciepła.

Wartość średnia całookresowa prądu przemiennego jest równa zero, dlatego podaje się wartość średnią pólokresową. Wartość tę można policzyć ze wzoru:

I_ŚR = (1/π) ₀∫^π/2 i(t)dt

Wartość średnia półokresowa prądu przemiennego jest równa takiej ilości prądu stałego który w tym samym czasie (połowie okresu) przeniesie taki sam ładunek co dany prąd przemienny.

Rozpatrując obwody prądu elektryczneg , możemy wyróżnić następujące elementy tych obwodów : odbiorniki o oporności czynnej i biernej. Do pierwszej grupy zaliczamy m. inn. rezystory , do drugiej zaś cewki i kondensatory.

Odbiornik o oporności czynnej to takie odbiorniki których indukcyjność oraz pojemność jest znikomo mała i można ją pominąć.

Prąd przepływający przez taki odbiornik wyrazi równanie:

i = I_m sin ωt

Spadek napięcia u na opornośći czynnej R przy jej niezmiennej wartości jest tym większy , im większa jest wartośc przepływającego prądu, więc chwilowe napięcie jest największe (U_m) w chwili, gdy wartośc chwilowa przepływającegoprądu i jest szczytowa (I_m) . Gdy prąd i = 0 , to napięcie u = 0. Napięcie i prąd na rezystancji są zgodne w fazie , osiągają w tych samych momentach swe wartości szczytowe dodatnie i ujemne oraz zerowe. Między prądem i napięciem chwilowym zachodzi związek:

u = R I_m sin ωt

A między wartościami szczytowymi:

U_m = R I_m

Wpływ pojemności na natężenie prądu zmiennego.

Napięcie doprowadzone do okładzin kondensatora o pojemności C zmienia się sinusoidalnie , tj. wg równania:

u = U_m sinωt

Prąd jaki będzie płynął przez kondensator związany będzie z przemieszczeniem ładunku q, dlatego możemy zapisać:

i = dq/dt

korzystając z równania:

dq = C du = C U_m ωcosωt dt

i biorąc pod uwagę dwa ostatnie związki:

i = C ωU_m cosωt

Mając na względzie, że:

cosα = sin(α+π/2)

otrzymujemy:

i = CωU_msin(ωt+π/2)

Rownanie to wskazuje , że przepływający przez pojemność prąd zmienny ma natężenie o przebiegu sinusoidalnym , które wyprzedza napięcie o kąt 90 ⁰. Szczytowa wartość natężenia prądu wynosi:

I_m = CωU_m , a dla wartości skutecznych : I = CωU

Kondensator przewodzi prąd zmienny . Stanowi on dla prądu zmiennego pewną oporność, której wartość wyraża się stosunkiem wartości skuyecznej napięcia U do prądu I. Oporność tę nazywa się opornością bierną poemnościową i oznacza X_C .

Xc = U/I = 1/ωC = 1/ (2πfC)

Wpływ indukcyjnośći na natężenie prądu zmiennego.

Jeżeli do żródła prądu stałego o napięciu U przyłączymy cewkę o indukcyności L o wielu zwojach z przewodu o znikomo małejm oporności , to przez taką zwjnicę mógłby teoretycznioe płynąć prąd o bardzo dużym natężeniu ograniczonym tylko opornością wewnętrzną żródła.

Jeżeli tą samą cewkę pozbawioną oporności czynnej przyłączymy do żródła prądu zmiennego, to okaże się , że natężenie tego prądu będzie ograniczone. Prąd w obwodzie ogranicza siła elektromotoryczna indukcji własnej e_L , której wartości są zależne od współczynnika indukcyjności własnej L zwojnicy i od szybkości zmian strumienia , a więc częstotliwości zmian prądu przepływającego przez uzwojenie cewki w myśl zależności:

e_L = - z dφ/dt lub e_L = - L di/dt

Gdy przez indukcyjnośc przepływa prąd zmienny , to wartość chwilową tego prądu wyraża równanie:

i = I_m sinωt

Spadek naięcia u_L na indukcyjności równoważy siłę elektromotoryczną indukciji własnej. Można to zapisać następuąco:

u_L = -e_L

Podstawiając za e_L równanie drfiniujące s.e.m. samoindukji oraz różniczkując wyrażenie na wartość chwilową prądu otrzymamy:

u_L = - e_L = L di/dt = LωI_m cosωt = LωI_msin(ωt + π/2)

Z powyższego równamia wynika , że napięcie doprowadzone do zacisków idealnej cewki wyprzedza prąd o 90 ⁰.

Bezwzględna wartość szczytowa napięcia na indukcyjności jest równa szczytowej wartości s.e.m. indukcyjności własnej:

U_m = E_m = LωI_m , A wartość skuteczna U = E = LωI

Ze wzoru wyrażającego zależność między wielkościami skutecznymi U , I i pulsacją ω prądu przepływającego , oraz indukcyjnością L odbiornika określamy tzw. oporność bierną indukcyjną X_L

X_L = U/I = ωL = 2πfL

Obwód szeregowy RLC.

Szeregowy obwód RLC składa się z szeregowo połączonych : rezystancji , indukcyjności i pojemności. Napięcie chwilowe między zaciskami zewnętrznej części takiego układu jest sumą algebraiczną napięć na poszczególnych częściach obwodu

u = u_R + u_L + u_C

Wartość skuteczna napięcia doprowadzonego do zacisków układu jest suma geometryczną napięć składowych U_L , U_R , U_C . Należy pamiętać o tym że napięcia U_L i U_C są przesunięte w fazie względem napoęcia U_R odpowiednio o + 90 ⁰ i - 90 ⁰. Poniższy rysunek przedstawia wykres wskazowy dla takiego przypadku:

U² = U_R² + (U_L - U_C)²

U = √ (IR)² + (IX_L - IX_C)² = I √ R² + (X_L - X_C)²

Wyrażenie pod pierwiastkiem nazywa się opornościaą pozoną (impedancją) i często oznacza się literą Z

Z = √ R² + (X_L -X_C)²

Jest to pierwastek z sumy kwadratów oporności czynnej i biernej , gdzie oporność bierna jest sumą geometryczną oporności biernej pojemnościowej i oporności biernej indukcyjnej występujących w obwodzie.

Obwody zasilane prądem zmiennym , zawierające elementy czynne i bierne powodują przesunięcia fazowe pomi®dzy prądem a napięciem. Kąt przesunięcia fazowego jest określony przez arctg stosunku oporności biernej od oporności czynnej:

ϕ = arctg (X_L - X_C)/R

Wzór wyrażający zależność między natężeniem prądu a napięciem :

I = U/Z

wyraża w najogólniejszej postaci prawo Ohma dla odcinka lub części zewnętrznej obwodu prądu przemiennego zawierającego oporność czynną i bierną .

WYKONANIE ĆWICZENIA

2a. Cewka bez rdzenia dla prądu stałego.

U [V]	1.75	3.5	5.25	7.0	8.75	10.75	12.5	13.2
I [A]	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.75
R [Ω]	17.5	17.5	17.5	17.5	17.5	17.9	17.9	17.6

2b. Cewka bez rdzenia dla prądu zmiennego.

U[V]	6	10.5	15	17	21	30	35
I[A]	0.3	0.5	0.7	0.8	1.0	1.4	1.6
Z[Ω]	20	21	21.4	21.3	21	21.9	31.3

2c. Cewka z rdzeniem dla prądu zmiennego.

U[V]	13	19	30	36	43	48	60	72
I[A]	0.2	0.3	0.5	0.6	0.7	0.8	1.0	1.2
Z[Ω]	65	63.3	60	60	61.4	60	60	60

2d. Kondensator dla prądu zmiennego.

U[V]	40	50	60	80	100	120	140	150
I[A]	0.11	0.15	0.18	0.25	0.32	0.39	0.45	0.48
Z[Ω]	363.6	333.3	333.3	340	312.5	307.7	311.1	312.5

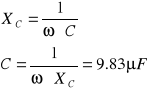
Obliczenia:

1. Dla cewki

%

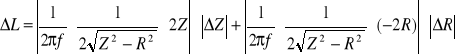
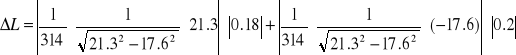
b) Dla kondensatora

=

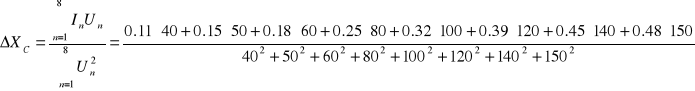
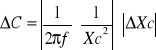
Wnioski :

Wyliczona wartość rezystancji cewki indukcyjnej wynosi R = 17.5Ω , natomiast jej impedancja bez rdzenia Z = 21.3Ω, odpowiednio z rdzeniem Z = 61.2Ω, w związku z czym można zauważyć iż rdzeń ferromagnetyczny wsunięty w uzwojenia selonoidu powoduje gwałtowny wzrost jego impedancji. Impedancja badanego kondensatora wynosi Z = 323.6Ω , element ten w przeciwieństwie do cewki dla napięć stałych stanowi rozwarcie.

U_C

U_L

U_R

U

U_L - U_C

---