Politechnika Śląska
Wydział Elektryczny
Kierunek EiT
Ćwiczenie laboratoryjne z fizyki :
Badanie szeregowego rezonansu napięciowego.
Grupa T2 sekcja 12
Paweł Jaskuła
Paweł Misiński
Marek Woźniczka
Gliwice 29.03.1999
Wprowadzenie.
Celem ćwiczenia jest wyznaczenie dobroci oraz rezystancji układu rezonansowego. Układ rezonansowy składa się z połączonych szeregowo : cewki indukcyjnej, opornika, kondensatora oraz generatora prądu przemiennego (siła wymuszająca). Prądem przemiennym nazywamy prąd, którego natężenie chwilowe zmienia się w czasie zgodnie z zależnością : gdzie : I0 - natężenie szczytowe [A]; ω - częstość [Hz]; t - czas [s]; φ - faza początkowa.
Przepływem prądu przemiennego, podobnie jak stałego, rządzą prawa Kirchoffa, lecz inaczej niż w obwodzie prądu stałego zachowują się kondensator i cewka. Prąd przemienny przepływa przez kondensator, przy czym przewodzenie prądu polega na ładowaniu kondensatora raz w jednym a za pół okresu przeciwnym kierunku. Napięcie UC na okładkach kondensatora wyraża się wzorem : gdzie : q - ładunek zgromadzony na okładkach kondensatora [C]; C - pojemność kondensatora [F]; ZC - impedancja kondensatora (opór jaki stawia on przepływowi prądu przemiennego) [Ω]; - kąt przesunięcia fazowego, o jaki jest przesunięte napięcie przemienne na kondensatorze w stosunku do natężenia prądu płynącego przez kondensator; . Moduł impedancji wyraża się wzorem : [Ω] .
W zachowaniu się cewki w obwodzie prądu przemiennego istotną rolę spełnia siła elektromotoryczna samoindukcji wyrażona wzorem : gdzie L - współczynnik samoindukcji cewki (cecha charakterystyczna) [H]; ZL - impedancja cewki (opór jaki stawia ona przepływowi prądu przemiennego) [Ω]; - kąt przesunięcia fazowego, o jaki jest przesunięte napięcie przemienne na cewce w stosunku do natężenia prądu płynącego przez cewkę. Moduł impedancji wyraża się wzorem : [Ω] .
Wielkością zwaną impedancją można posługiwać się analogicznie do rezystancji w obwodach prądu stałego. W przypadku obwodu złożonego z szeregowo połączonych opornika, kondensatora oraz cewki moduł impedancji wyraża się wzorem : . Na podkreślenie zasługuje fakt, iż posługiwanie się pojęciem impedancji w obwodach prądu przemiennego umożliwia rozwiązywanie wielu zagadnień poprzez konstrukcję wektorowych wykresów napięć na elementach obwodu RLC.
Związek pomiędzy amplitudą natężenia prądu płynącego przez obwód szeregowy a amplitudą i częstotliwością przyłożonego napięcia wyraża się wzorem : gdzie U0 - napięcie wymuszające. Krzywa będąca wykresem zależności amplitudy natężeń prądu płynącego przez obwód RLC jako funkcję częstotliwości przyłożonego napięcia nosi nazwę krzywej rezonansowej. Amplituda natężenia osiąga wartość maksymalną w warunkach rezonansu, to jest gdy częstotliwość zmian przyłożonego napięcia odpowiada tzw. częstości rezonansowej układu wyrażającej się wzorem : . W warunkach rezonansu spadki napięć na kondensatorze mają jednakowe wartości oraz przeciwne fazy, czyli się znoszą. Moduł impedancji wyraża się wtedy wzorem : gdzie R - opór w układzie RLC. Można więc w warunkach rezonansu wyznaczyć opór układu : .
Jakość układu rezonansowego opisuje tzw. współczynnik dobroci układu Q. Jest to pomnożony przez 2Π stosunek maksymalnej energii zgromadzonej w obwodzie do energii traconej w ciągu jednego okresu. Dobroć układu RLC wyraża się wzorem : . Wartość Q można także określić z przebiegu krzywej rezonansowej : jest ona równa stosunkowi częstotliwości rezonansowej ωR do szerokości połówkowej krzywej mierzonej w dla natężenia .
Opis przebiegu ćwiczenia.
Łączymy obwód według schematu.
Ustalamy parametry początkowe :
pojemność kondensatora C=60 [nF]
indukcyjność cewki L=400 [mH]
napięcie zasilające układ U0 = 3 [V]
Zmieniając częstotliwość generatora co 50 [Hz] w przedziale 200÷2000 [Hz] notujemy wskazania mierników. W otoczeniu rezonansu wykonujemy pomiary co 10 [Hz].
Schemat układu pomiarowego.
Tabela pomiarowa.
Spis przyrządów pomiarowych.
Opracowanie wyników pomiarów.
Obliczenia błędu pomiarowego.
Obliczenia dla rezystancji:
Obliczenia dla dobroci metodą szerokości połówkowej:
Obliczenia dla dobroci metodą teoretyczną:
Podsumowanie.
f [Hz] |
i [mA] |
UL [V] |
UC[V] |
200 |
0,21 |
0,11 |
3,15 |
250 |
0,28 |
0,19 |
3,22 |
300 |
0,35 |
0,28 |
3,31 |
350 |
0,43 |
0,40 |
3,43 |
400 |
0,51 |
0,54 |
3,56 |
450 |
0,61 |
0,72 |
3,74 |
500 |
0,72 |
0,94 |
3,96 |
550 |
0,85 |
1,21 |
4,23 |
600 |
1,01 |
1,56 |
4,57 |
650 |
1,20 |
2,00 |
5,00 |
700 |
1,44 |
2,57 |
5,55 |
750 |
1,76 |
3,36 |
6,31 |
800 |
2,18 |
4,41 |
7,34 |
850 |
2,82 |
6,06 |
8,86 |
900 |
3,76 |
8,51 |
11,12 |
950 |
5,20 |
12,40 |
14,55 |
960 |
5,57 |
13,41 |
15,39 |
970 |
5,94 |
14,45 |
16,23 |
980 |
6,28 |
15,41 |
17,00 |
990 |
6,66 |
16,41 |
17,73 |
1000 |
7,01 |
17,48 |
18,44 |
1010 |
7,22 |
18,14 |
18,81 |
1020 |
7,36 |
18,67 |
18,97 |
1028 |
7,39 |
18,90 |
18,90 |
1030 |
7,40 |
18,92 |
18,88 |
1040 |
7,32 |
18,97 |
18,52 |
1050 |
7,17 |
18,66 |
17,96 |
1060 |
6,83 |
18,05 |
16,91 |
1080 |
6,34 |
16,96 |
15,42 |
1100 |
5,61 |
15,34 |
13,38 |
1150 |
4,33 |
12,31 |
9,87 |
1200 |
3,41 |
10,11 |
7,43 |
1250 |
2,85 |
8,77 |
5,98 |
1300 |
2,43 |
7,76 |
4,90 |
1350 |
2,10 |
6,97 |
4,07 |
1400 |
1,85 |
6,37 |
3,44 |
1450 |
1,68 |
5,96 |
3,01 |
1500 |
1,53 |
5,44 |
2,44 |
1550 |
1,40 |
5,31 |
2,34 |
1600 |
1,30 |
5,06 |
2,09 |
1650 |
1,22 |
4,88 |
1,90 |
1700 |
1,13 |
4,69 |
1,70 |
1750 |
1,08 |
4,57 |
1,58 |
1800 |
1,01 |
4,45 |
1,46 |
1850 |
0,97 |
4,33 |
1,33 |
1900 |
0,92 |
4,23 |
1,23 |
1950 |
0,88 |
4,14 |
1,14 |
2000 |
0,85 |
4,06 |
1,07 |
Amperomierz - Multimetr V561 (0,5%),
Woltomierz UL - Multimetr V561 (0,5%),
Woltomierz UC - Multimetr V561 (0,5%),
Częstościomierz HC-81 (0,1%),
Power generator PO-28
Dekada indukcyjnościowa
Dekada pojemnościowa DK50
Na podstawie tabeli rysujemy wykres zależności natężenia prądu od częstotliwości oraz zależności napięcia UL i UC od częstotliwości. Z wykresu natężenia prądu w funkcji częstotliwości odczytujemy maksymalne natężenie prądu płynącego w obwodzie IMAX oraz odpowiadającą mu częstotliwość rezonansową fR:
IMAX = 7,40 [mA]
fR = 1030 [Hz]
Następnie, w celu obliczenia dobroci układu metodą szerokości połówkowej, obliczamy :
oraz odczytujemy częstotliwości, dla których I=IQ :
f1 = 951 [Hz] f2 = 1116 [Hz]
Δf = 1116-951 = 165 [Hz]
więc :
Następnie obliczamy rezystancję układu :
Korzystając z wyliczonej rezystancji R, obliczamy dobroć układu :
Błąd liczę metodą różniczki zupełnej :
Mamy :
U0 = 3 [V]
ΔU0 = 0,5% wskazania = 0,015 [V]
IMAX = 0,0074 [A]
Δ IMAX = 0,0074 = 0,000037 [A]
Więc :
czyli
R = 405,41 ± 4,05 [Ω]
Mamy :
fR = 1030 [Hz]
ΔfR = 0,1% wskazania = 0,1% ⋅ 1030 = 1,03 [Hz]
Δf = 165 [Hz]
Δ (Δf) = 0,2![]()
165 = 0,33 [Hz]
Więc :
czyli
Q = 6,24 ± 0,02
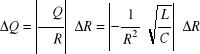
Mamy :
R = 405,41 [Ω]
ΔR = 4,05 [Ω]
L = 0,400 [H]
C = [F]
Więc :
czyli
Q = 6,37 ± 0,06
Na podstawie wykonanych przez nas pomiarów otrzymaliśmy następujące wyniki:
Częstotliwość rezonansowa układu wynosi:
fR = 1030 ± 1 [Hz]
Wyliczona rezystancja obwodu rezonansowego wynosi :
R = 405,41 ± 4,05 [Ω]
Dobroć obwodu wyliczona metodą szerokości połówkowej wynosi :
Q = 6,24 ± 0,02
Dobroć obwodu wyliczona ze wzoru analitycznego wynosi :
Q = 6,37 ± 0,06
Jak widać , dobroć obwodu wyliczona metodą analityczną różni się od dobroci wyznaczonej na podstawie pomiarów, a różnica ta przekracza zakres obliczonych błędów pomiarowych. Na mniejszą, w stosunku do wyliczeń analitycznych, dobroć układu mogły wpłynąć nie uwzględnione w rachunkach pojemności i indukcyjności powstałe na skutek podłączenia mostka LC do obwodu pomiarowego za pomocą przewodów , oraz różnice pomiędzy wartościami wskazywanymi przez mostek, a faktycznymi wartościami pojemności i indukcyjności .
Zależności prądu oraz napięć na kondensatorze i cewce indukcyjnej zostały przedstawione na wykresach . Można zauważyć , że krzywa przedstawiająca Uc = f(f) wyraźnie przypomina krzywą UL = f(f) odbitą symetrycznie względem prostej f = fr , gdzie fr - częstotliwość rezonansowa układu.
Badanie szeregowego rezonansu napięciowego.
- 7 -
Wyszukiwarka
Podobne podstrony:
Badanie szeregowego rezonansu napięciowego, Badanie szeregowego rezonansu napięciowego 5, Politechni
Badanie szeregowego rezonansu napięciowego, Badanie szeregowego rezonansu napięciowego 4, Politechni
Rezonator kwarcowy, Rezonator kwarcowy 3, Politechnika Śląska
Rezonator kwarcowy, Rezonator kwarcowy 1, POLITECHNIKA ŚLĄSKA
KARTA INSTRUKCYJNA OBROBKI2, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Se
17 listopada, Politechnika Śląska semestr I GiG, Górnictwo
wzory Finanase przedsiebiorstw, Politechnika Śląska ZiIP i inne, Finanse
czystakartainstrukcyjnaobrobki, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL,
Rozk ad labów, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Inżynierskie, Se
Politechnika Śląska sprawko moje (Naprawiony)
Politechnika śląska w gliwicach sprawko na dziekana
podstawowe informacje o ochronie prawnej wzorów przemysłowych, Studia - Politechnika Śląska, Zarządz
Projekt (chemia), Uczelnia - Politechnika Slaska, Chemia, Chemia
Testy 5 ekonomika podatkowa, Politechnika Śląska ZiIP i inne, Ekonomika podatkowa
ściąga ciocia, Uczelnia - Politechnika Slaska, Petro Węgla
odp zestaw e, Politechnika Śląska MT MiBM, Semestr III, Bazy danych
więcej podobnych podstron