Politechnika Lubelska		Laboratorium technologii włókien i kabli światłowodowych
w Lublinie
Nazwisko: Szyszkiewicz Maliszewski Pławski	Imię: Andrzej Jacek Paweł		Semestr ΙΧ	Grupa ED. 9.3	Rok akad. 1998/99
Temat ćwiczenia: Pomiar właściwości mechanicznych światłowodów				Data wykonania	Ocena

1. Pomiar wytrzymałości na zerwanie włókien światłowodowych.

W ćwiczeniu wykonano próbę wytrzymałości na zerwanie włókien światłowodowych.

Próbie poddano 25 włókien z pokryciem niecentrycznym i 25 włókien z pokryciem centrycznym. Pomiary przeprowadzono na wyciągarce Tiratest 2200, a uzyskane wyniki w postaci wydruku komputerowego stanowią załącznik do sprawozdania.

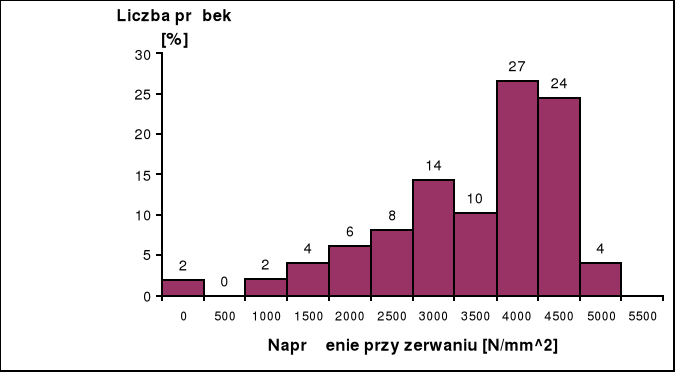
Wyznaczenie histogramów

Na podstawie uzyskanych wyników pomiarów sporządzono poniższą tabelę i procentową liczbę próbek, które zostały zarwane przy danym zakresie naprężeń.

s	liczba próbek
[N/mm^2]	szt.	%
0-500	0	1
500-1000	0	0
1000-1500	1	2
1500-2000	2	4
2000-2500	3	6
2500-3000	4	8
3000-3500	7	14
3500-4000	5	10
4000-4500	13	27
4500-5000	12	24
5000-5500	2	4

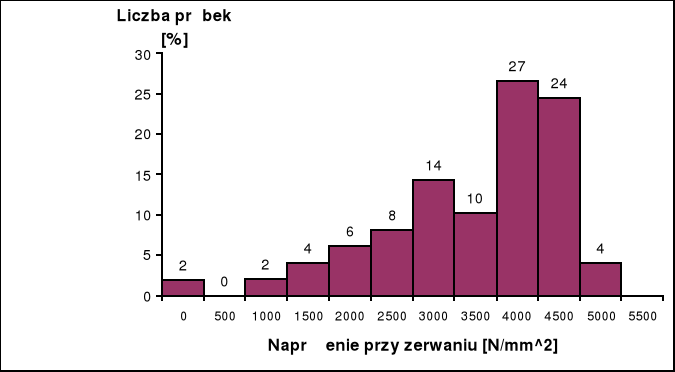
Histogram

Wyznaczanie wykresu Weibulla

Punkty wykresu wyznaczono na podstawie pomiarów naprężenia przy zerwaniu, a przedstawia je poniższa tabela ( s- naprężenie, x- numer próbki )

Ln s	4,65	6,92	7,47	7,59	7,60	7,76	7,80
Ln[Ln(50/(50-x))]	-3,90	-3,20	-2,78	-2,48	-2,25	-2,06	-1,89
Ln s	7,94	7,94	7,95	7,99	8,01	8,01	8,03
Ln[Ln(50/(50-x))]	-1,75	-1,62	-1,50	-1,39	-1,29	-1,20	-1,11
Ln s	8,03	8,04	8,04	8,14	8,17	8,20	8,26
Ln[Ln(50/(50-x))]	-1,03	-0,95	-0,88	-0,81	-0,74	-0,67	-0,61
Ln s	8,26	8,28	8,30	8,33	8,33	8,34	8,34
Ln[Ln(50/(50-x))]	-0,55	-0,48	-0,42	-0,37	-0,31	-0,25	-0,20
Ln s	8,36	8,37	8,38	8,38	8,39	8,39	8,40
Ln[Ln(50/(50-x))]	-0,14	-0,09	-0,03	0,02	0,08	0,13	0,19
Ln s	8,41	8,42	8,46	8,46	8,46	8,47	8,48
Ln[Ln(50/(50-x))]	0,24	0,30	0,36	0,41	0,48	0,54	0,61
Ln s	8,48	8,48	8,48	8,49	8,49	8,50	8,53
Ln[Ln(50/(50-x))]	0,68	0,75	0,83	0,93	1,03	1,17	1,36

Wykres Weibulla

Wyznaczanie współczynnika m

Otrzymany wykres Weibulla można rozpatrywać przedziałami ( jest złożeniem kilku prostych ). Współczynnik nachylenia danej prostej jest równy parametrowi m. Obecność kilku parametrów świadczy o różnych przyczynach pęknięci włókna. Wyliczyłem parametr m dla jednej prostej.

2. Przeprowadzanie testu na odporność ( proof-test ).

Proof-test wykonano dla włókna światłowodowego o parametrach:

długość: l = 240 m

średnica: φ = 125 μm ⇒ przekrój włókna: A= 0.0123 mm²

długość odcinka włókna poddawany naprężeniu: l₁ = 0,9 m

czas rozciągania włókna: t = 2 m/s

siła rozciągająca: F = 10 N

Naprężenie działające na włókno podczas proof - testu:

W wyniku przeprowadzenia proof - testu nie można zagwarantować, że badane włókno będzie spełniało parametry nie na całej długości ( zanotowano 4 pęknięcia )

Korzystając z wyników pomiarów przeprowadzonych w ćwiczeniu oraz założenia, że dla badanego włókna parametr n = 94.36, można wyznaczyć parametry uproszczonego wzoru na czas życia włókna światłowodowego:

log t = B- n* log s

B = log t + n*log s =log 2 + 94,36*log(813) ≈ 274,6

więc

log t = 274,6- 94,36* log s

3. Rozwiązywanie zadań

1. Wyznaczyć czas życia badanego włókna światłowodowego, na które działa siła naprężająca równa 3 N.

Dane: Szukane:

F = 3 N t = ?

φ = 0,125 μm ⇒ A = 0,0123 mm²

n = 90 + m = 90 + 4,36 = 94,36

B = 274,6

log t = 274,6 - 94,36*log s ⇒ t =
=
=

Odp. Czas życia wynosi

2. Sprawdzić czy badane włókno może być użyte do produkcji żyroskopu o średnicy d = 3 cm, który ma być sprawny co najmniej przez okres 5 lat.

Dane: Szukane:

d = 3 cm ⇒ r =60 mm t = f(s)

n = 94,36

B = 274,6

Odp. Badane włókno można zastosować do budowy zakładanego żyroskopu

4