Laboratorium Podstaw Elektrotechniki Politechniki Lubelskiej

Wykonawcy: Wiesław Rycerz , Tomasz Sugier Lesław Widz						Symbol grupy ED 4.5
Data wyk. Ćwiczenia 1997-03-17 1997-03-24		Symbol ćwiczenia: 5 a,bc		Temat zadania Modelowanie pól płaskich na papierze elektroprzewodzącym i symulacja tych pól na komputerze
	ZALICZENIE			Ocena	Data	Podpis

Cel ćwiczenia:

Zapoznanie się z kształtem pól i ich właściwościami dla różnych kształtów przewodnika. Symulacja tych pól na komputerze i wyznaczanie różnych wielkości polowych.

Przyrządy użyte w ćwiczeniu:

• woltomierz typ V540;

• generator prądu stałego KB-60-01;

• pantograf wraz z sondą;

• papier elektroprzewodzący;

• amperomierz ( klasa 0,5; zakres 30mA; WSInż-EP-43-3/1466; 3403074.76 );

• komputer ( program QuickField ).

Wykonanie ćwiczenia:

Modelowanie pól płaskich na papierze elektroprzewodzącym.

Schemat układu pomiarowego.

Uzyskane wykresy linii ekwipotencjalnych są narysowane na załączonych kartkach papieru kancelaryjnego.

Pomiary wykonano dla napięcia U=10V

Wartości prądu przy badaniu poszczególnych pól:

układ walców współosiowych I=27mA;

układ walcowy ( metoda zadania odwrotnego ) I=3,5mA;

układ przewodnika o zmiennym przekroju I=2mA;

2. Wyznaczanie różnych wielkości polowych dla kabla koncentrycznego:

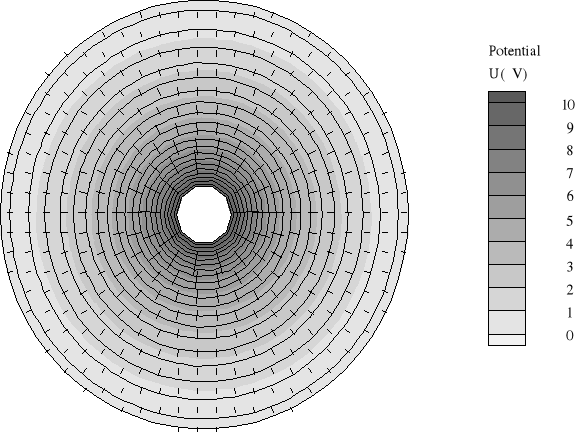
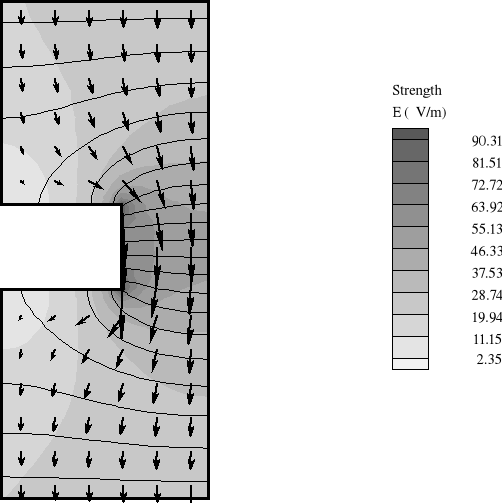
rozkład linii ekwipotencjalnych;

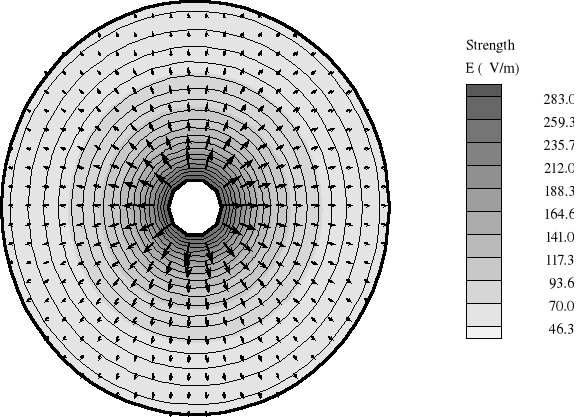
mapa i wektory natężenia pola elektrycznego

punkty a) i b);

Rysunek do punktów a), b) i c)

1. 
   

1. Sprawdzenie prawa Gaussa - całkowanie po powierzchni ( linie 1 i 2 );

1. powierzchnia wyznaczona przez linię1 Q₁=-1.6e-13 C

1. powierzchnia wyznaczona przez linię2 Q₂ = 2.819e-10 C

1. Z wyników widać, że ładunek w powierzchni zamkniętej ( 2 ), w której znajduje się źródło pola jest trzy rzędy wielkości większy niż przez powierzchnię zamkniętą (1),

1. w której nie ma źródła pola. Dlatego możemy przyjąć, że ładunek 1 jest równy zero.

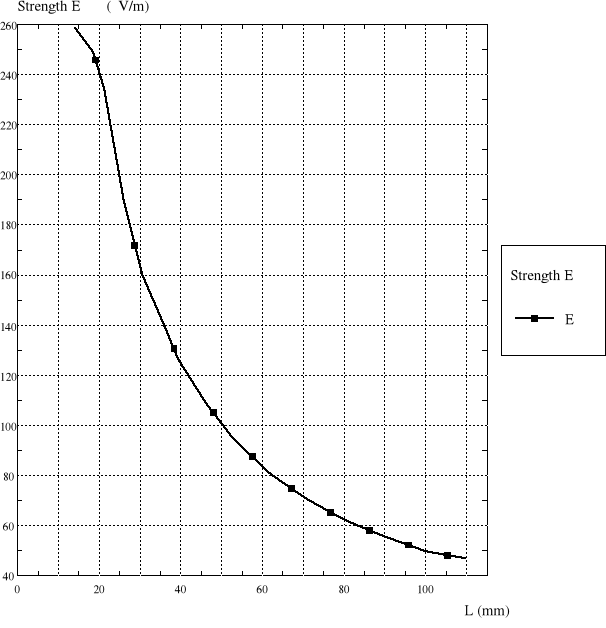
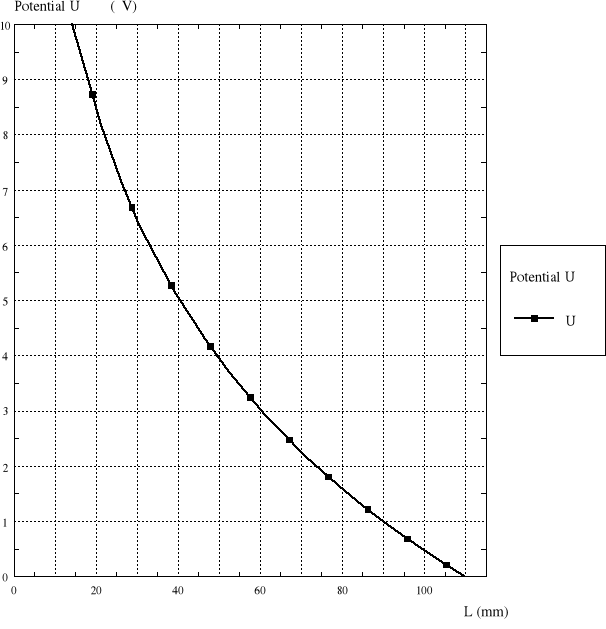
rozkład natężenia pola elektrycznego i potencjału wzdłuż promienia;

3. Pole przepływowe w układzie walcowym:

rozkład linii ekwipotencjalnych;

mapa i wektory natężenia pola elektrycznego

punkty a) i b);

Rysunek do punktów a), b) i c)

1. 
   

a) mapa i obraz wektorów gęstości prądu

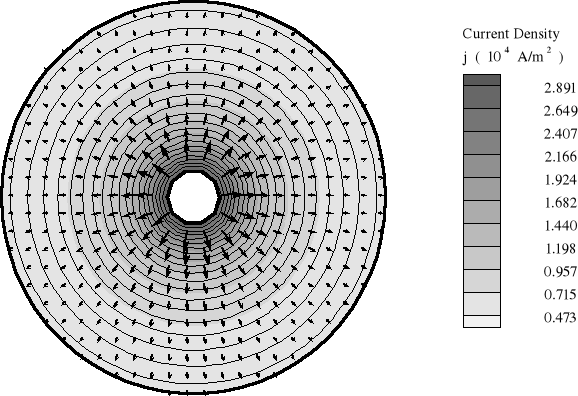
1. sprawdzenie I prawa Kirchoffa - obliczanie całki po powierzchni 1. I = -1.8415 A/m.

wartość prądu płynącego pomiędzy elektrodami , całkując po powierzchni 2 I=3300A/m.

Rozpatrują przypadki f i g możemy stwierdzić, że I prawo Kirchhoffa jest spełnione, gdyż wartość prądu w przypadku f jest znacznie mniejsza od wartości w punkcie g i wolno nam przyjąć jego wartość jako równą zero.

rezystancja przejścia na podstawie wartości prądu obliczonej w punkcie g i wartości napięcia między elektrodami U=10V

R_o= U/I = 10V / 3300A = 0,003 W.

4. Wyznaczanie linii sił pola w układzie walcowym metodą zadania odwrotnego:

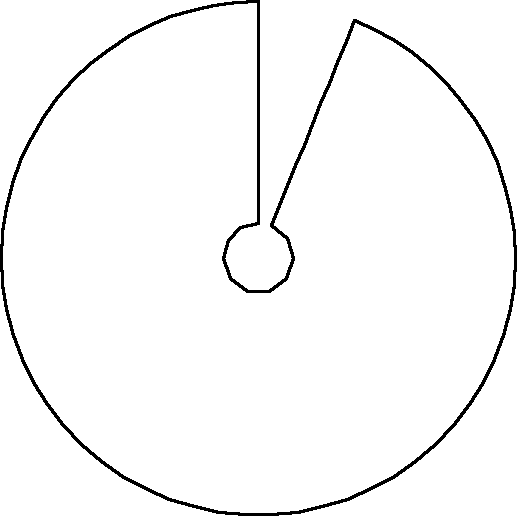
a) rozkład linii ekwipotencjalnych

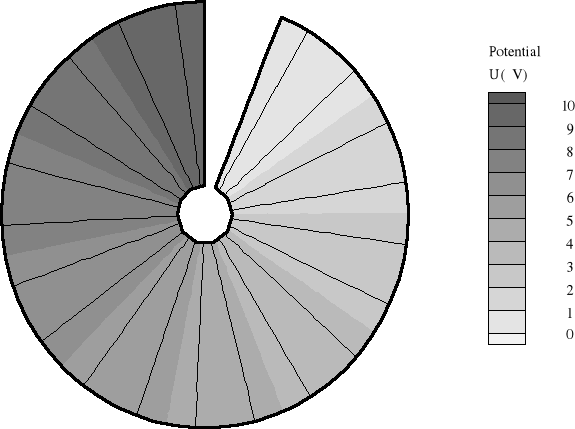
W metodzie zadania odwrotnego linie ekwipotencjalne są prostopadłe w porównaniu do metody normalnej, a jednocześnie są równoległe do wektorów natężenia pola elektrycznego w tym przypadku. Natomiast wektory natężenia pola elektrycznego w metodzie odwrotnej są prostopadłe do wektorów wyznaczanych w metodzie normalnej. Natomiast ich kierunki pokrywają się ze stycznymi linii ekwipotencjalnych z metody normalnej.

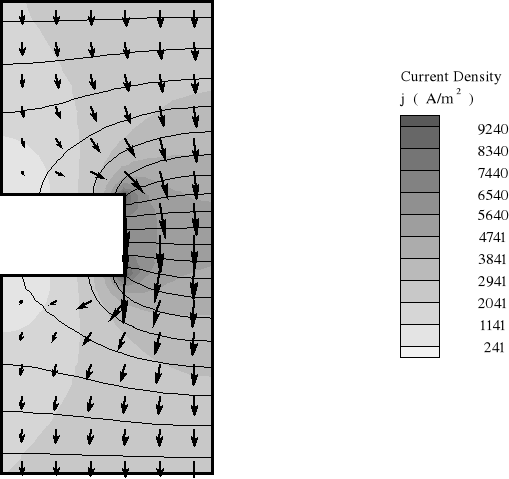
5. Pole przepływowe w przewodniku o zmiennym przekroju:

rozkład linii ekwipotencjalnych;

mapa i wektory natężenia pola elektrycznego

punkty a) i b);

Rysunek do punktów a), b) i c)

mapa i obraz wektora gęstości prądu

Wnioski:

W wykonanym ćwiczeniu dokonywaliśmy modelowania pól płaskich na papierze elektroprzewodzącym, a następnie dokonaliśmy komputerowej symulacji tych pól. Porównując wyniki z obu doświadczeń możemy zauważyć, że linie ekwipotencjalne wyznaczone podczas pomiarów z użyciem sondy i pantografu są niemal identyczne z liniami wyznaczonym na komputerze.

Korzystając z metody zadania odwrotnego dla układu walców współosiowych mogliśmy, korzystając tylko z linii ekwipotencjalnych ( które są do siebie wzajemnie prostopadłe ), wyznaczyć linie sił pola elektrycznego, które są prostopadłe do linii ekwipotencjalnych danego pola i pokrywały się z liniami ekwipotencjalnymi pola drugiego.

Podczas symulacji komputerowej mogliśmy też stwierdzić słuszność prawa Gaussa i I prawa Kirchhoffa. Otrzymane wyniki nie odzwierciedlały dokładnie tych praw, ale błąd był bardzo niewielki i z dość dużą dokładnością można było stwierdzić zgodność teorii z praktyką.

---