Dyspersja i straty energii w polu elektrycznym

Straty dielektryczne: przewodnościowe, wskutek ruchu jonów w polu elektrycznym,

polaryzacyjne , wskutek obrotu dipoli w polu elektrycznym

Mechanizmy i rodzaje polaryzacji

Charak-terystyka	Mechanizm		Rodzaj Wpływ temperatury
		Bez pola elektrycznego (E = 0)		W polu elektrycznym (E > 0)
Indu-kowane Rezonan-sowe			a) elektronowa, w obszarze atomu, nie ma wpływu temperatury
			b) atomowa w obszarze cząsteczki, nie ma wpływu temperatury
Trwałe Relaksa-cyjne			c) dipolowa, orientacja trwałych dipoli, wpływ temperatury
			d) ładunku przestrzennego, wpływ temperatury

Straty polaryzacyjne:

Obrót dipoli: - indukowanych

- trwałych

w otoczeniu cząsteczek materiału ⇒ energia cieplna pobrana i rozproszona na podwyższenie temperatury

Schemat zastępczy przedstawiający straty przewodnościowe

Schemat zastępczy przedstawiający straty polaryzacyjne:

Charakterystyki ε' i ε'' schematu zastępczego przedstawiającego straty polaryzacyjne:

Charakterystyki ε' i ε'' schematu zastępczego przedstawiającego straty przewodnościowe

Schemat pełny dielektryka ze stratami przewodnościowymi i czterema rodzajami strat polaryzacyjnych

Rzeczywisty kondensator

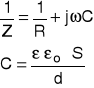
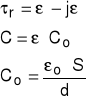
(1)

(2)

1. i (2):

Konduktywność dielektryków

Ruchliwość jonów

μ - ruchliwość, m2V-1s-1

e = 1,62⋅10-19 C

μ = 10-4 ÷10-14 dielektryku

μ = 10 ÷10-4 metale, półprzewodniki

Zależność temperaturowa konduktywności dielektryków

Energia cząsteczek:

- prędkość średnia kwadratowa,

R - stała gazowa R = 8,314 J⋅K-1 mol-1

NA - stała Avogadro A = 6,02 1023 atomów/mol

Oznaczenie:

, stała Boltzmanna k = 1,38⋅10-23 JK-1 = 0,856 10-4 eVK-1

kT = 0,023 dla K = 398K

Jeśli liczba cząsteczek mających energie pomiędzy W i W+dW wynosi N(W) dW, prawdo-podobieństwo, że dana cząsteczka ma tę energię wynosi:

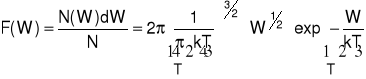
Jest to rozkład Maxwella-Boltzmanna

Wpływ temperatury występuje w dwu czynnikach powyższego wzoru , lecz drugi przeważa.

Wm - energia średnia

Rozkład Maxwella-Boltzmanna energii cząsteczek

Ruch cząsteczek przekraczających barierę energetyczną W' w jednostce czasu wynosi:

S - stała

Jest to równanie Arrheniusa

w dielektrykach:

n - liczba lub ruchliwość jonów lub elektronów

dokładniej:

Nośniki prądu w dielektrykach

Gazy

ujemne elektrony

dodatnie jony

lub

ujemne naładowane molekuły (np. zanieczyszczenia - - elektrofiltry)

Ciecze

ujemne elektrony

dodatnie jony

lub naładowane molekuły

ujemne naładowane cząsteczki

Ciała stałe

ujemne elektrony poprzez pasmo dozwolone

dodatnie drobiny poprzez pasmo zabronione

dodatnie jony zabronione

lub

ujemne naładowane molekuły

Mechanizm elektronowy przewodnictwa w dielektrykach stałych

energia

dozwolone

zabronione

dozwolone

zabronione

dozwolone

odległości atomów

Kontakt izolator/metal

Typowe wartości prac wyjścia metalu i dielektryka w 20°C

Dielektryk	φd [eV]	Metal	φm [eV]
Polistyren Polwęglan Szkło BrAlSi Poliimid Czysty Al2O3 Czysty SiO2	4,2 4,3 4,3 4,4 ~ 5 ~ 6	Cs Mg Al Ag Ni Au	1,9 3,8 4,2 4,3 4,7 4,9

Przewodnictwo tunelowe

Przewodnictwo jonowe w dielektrykach stałych

? Wakansy (ładunek -1) ? Nadmiary (ładunek +1)

Na+ Cl-1 Na+ Na+ Cl- Na+

Cl- Cl- Cl- Na+ Cl-

Na+ Cl- Na+ Na+ Cl-1 Na+

n - liczba jonów/jedn.obj.,

ze - ładunek jonu,

μ - ruchliwość

ruch ładunków (jonów)

Ruch dyfuzyjny jonów w przeciwnym kierunku:

x

E

ruch jonów pod wpływem E

←- - - - ruch jonów pod wpływem dyfuzji

Równowaga:

D - współczynnik dyfuzji

Charakterystyki

j = f(E)

dielektryków

POLE ELEKTRYCZNE

GAZY

POLE ELEKTRYCZNE

CIECZE

POLE ELEKTRYCZNE

CIAŁA STAŁE

1

11

dysper~1.doc

R1

C1

U

J

J

U

JR

Jc

δ

tgδ

ω

J

U

C2

R2

δ

JXC2

JR2

U

J

δ

tgδ

ω

ε"

C

Cp

Rp

ε'

CR

RR

ε"

ε'=const

f

C

Cpm

RR

Cpol

Cpd

Cpi

Rpol

Rpm

Rpi

Rpd

C

R

S

d

ε',ε"

ε'

ε"

lnf

F(W)

W/Wm

0

1/3

1,0

2,0

ln n

1/T

metal

metal

dielektryk

poziom próżnia

pasmo

przewodnictwa

poziom Fermiego

praca wyjścia

praca

wyjścia

pasmo

zabronione

Energia

φd

φm

Hopping

Na+

(pomiędzy pułapkami)

Silne

E

j

Słabe

E

tunelowe

dielektryk

metal

metal

j

Silne

Słabe

E

j

Silne

Słabe

U

i

S

d

---