10742 skanuj0106 (23)

V. ZGINANIE UKOŚNE

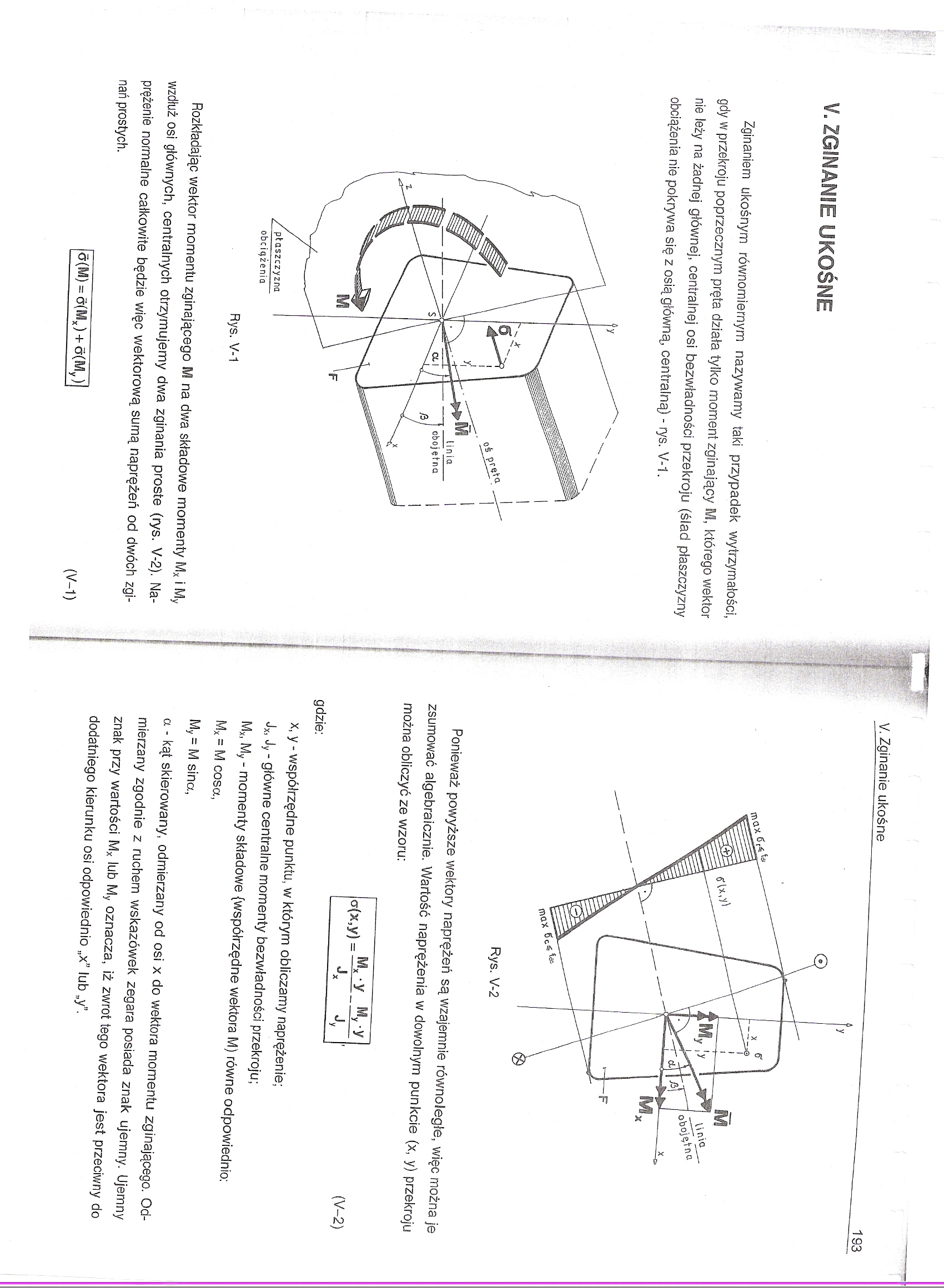
Zginaniem ukośnym równomiernym nazywamy taki przypadek wytrzymałości, gdy w przekroju poprzecznym pręta działa tylko moment zginający M, którego wektor nie leży na żadnej głównej, centralnej osi bezwładności przekroju (ślad płaszczyzny obciążenia nie pokrywa się z osią główną, centralną) - rys. V-1.

Rys. V-1

Rozkładając wektor momentu zginającego M na dwa składowe momenty M_x i M_y wzdłuż osi głównych, centralnych otrzymujemy dwa zginania proste (rys. V-2). Naprężenie normalne całkowite będzie więc wektorową sumą naprężeń od dwóch zgi-nań prostych.

a(M) = ó(M_x) + 6(M_y)

(V-1)

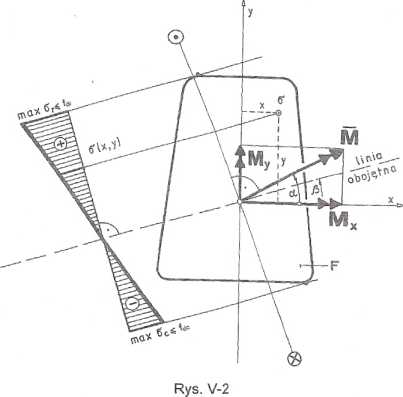
Ponieważ powyższe wektory naprężeń są wzajemnie równoległe, więc można je zsumować algebraicznie. Wartość naprężenia w dowolnym punkcie (x, y) przekroju można obliczyć ze wzoru:

a(x,y) =

M_xy

M_yy

J„

(V-2)

gdzie:

x, y - współrzędne punktu, w którym obliczamy naprężenie:

Jx, Jy - główne centralne momenty bezwładności przekroju;

M*, M_y - momenty składowe {współrzędne wektora M) równe odpowiednio: M_x = M cosa,

a - kąt skierowany, odmierzany od osi x do wektora momentu zginającego. Odmierzany zgodnie z ruchem wskazówek zegara posiada znak ujemny. Ujemny znak przy wartości M_x lub M_y oznacza, iż zwrot tego wektora jest przeciwny do dodatniego kierunku osi odpowiednio _Bx” lub „y”.