12489 skanuj0276 (4)

Obliczamy teoretyczny i praktyczny współczynnik przesunięcia zarysu:

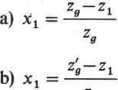
17-9

17

14-9

17

'9

= 0,4706

= 0,294

Na podstawie tablicy 11.3 stwierdzamy, że w przypadku a) wartość x₁ je?*, zbliżona do wartości grożącej nadmiernym zaostrzeniem zębów i dlatego decydujemy się na niewielkie podcięcie, przyjmując x_t = 0,294.

Obliczamy przesunięcie zarysu

X_y = Xy m = 0,294-6 = 1,764 mm

Przyjmujemy Xy = 1,8 mm oraz X₂ = —1,8 mm (aby uniknąć wykonywania średnic kół ze zbyt dużą dokładnością).

Obliczamy wymiary zębów i kół:

dy = m-Zy =6-9 — 54 mm

d_al = m(z + 2) + 2X = 6(9+ 2)+ 2-1,8 = 69,6 mm

d_fy = m(z-2,5) + 2X = 6(9-2,5)+ 2-1,8 = 42,6 mm

Ky	= m + X = 6+1,8 =	7,8 mm
hj-y	= 1,25 m-X - 1,25	>/~r ii oo 7
d2 -	= 6-35 = 210 mm
dal	= 6(35 + 2)—2-1,8 =	218,4 mm
df2	= 6(35-2,5)-2-1,8	= 191,4 mm
Ki	= 6 —1,8 = 4,2 mm
h/2	= 1,25-6 + 1,8 = 9,3	mm
ar =	--a = 0,5(54 + 210) =	132 mm

PRZYKŁAD 11.5. Przekładnię o parametrach: z_x = 19, z₂ = 47, m = 5 mm, a₀ = 20° należy zastosować w urządzeniu, w którym odległość osi wałów wynosi a_r = 170 mm. Obliczyć wymiary kół.

Rozwiązanie

Obliczamy teoretyczną odległość osi dla projektowanej przekładni a — 0,5 m(zy +z₂) -- 0,5-5(19 + 47) = 165 mm

W celu dostosowania przekładni do istniejącej odległości wałów a_r = 170 mm należy zastosować koła z dodatnim przesunięciem zarysu.

Obliczamy wartość współczynnika B_r z zależności a_r = a + B_r • a

Otrzymujemy

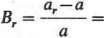
170-165

165

= 0,03030

276