154 155

■ aBD ł Bc + BCD + BCE rn BOD + BD + CDE » XBD + Bc® + BCD + CDS

łączna liczba różnych impllkantów prostych tworzących zadana funkcja wynosi 15, a więc w tej postaci funkcji tych nie da się zrealizować za pomocą nadanej FU (nie istniejącej w rzeczywistości, a. tylko założonej dla tego przykładu). Jeżeli Jednak spróbujemy zrealizować negację funkcji f 1 wraz z pozostałymi funkcjami wyrazić Ją nie za pomocą impllkantów prostych, lecz, przerywając minimalizację na etapie wcześniejszym, za pomocą impllkantów bardziej rozbudowanych, to otrzymamy

6    7

+ ABCD + ABCD

1    2    3    4

f₁ ■ IBRD + BCD + BCD + BCDE + A

7    10

ABC® + BCDE

8    2    9    4    5    6

IBcB + BCD + IBCOE + BCDE + ABCBS + ABCD -

1    11    3

IBCB + BCDE + BCD +

4    10    6

BCDE + BCDE + ABCD

1 a _    3    4    12    7

IBCB + IBCD + BCD ♦ BCDS + BCDE + aBc®

Takie przedstawienie zadanych funkcji wymaga tylko 12 iloczynów,a więc Jest realizowalne. (Liczbę koniecznych iloczynów można zmniejszyć Jeszcze

								MATMA m
I ^
I ^
^ L±___
	)	I J	( 5	t r	i «	• N	_V>IF	=4., =4,, 4r,
NATfkCA OR							—v>°*v
							„jsJrs
	k

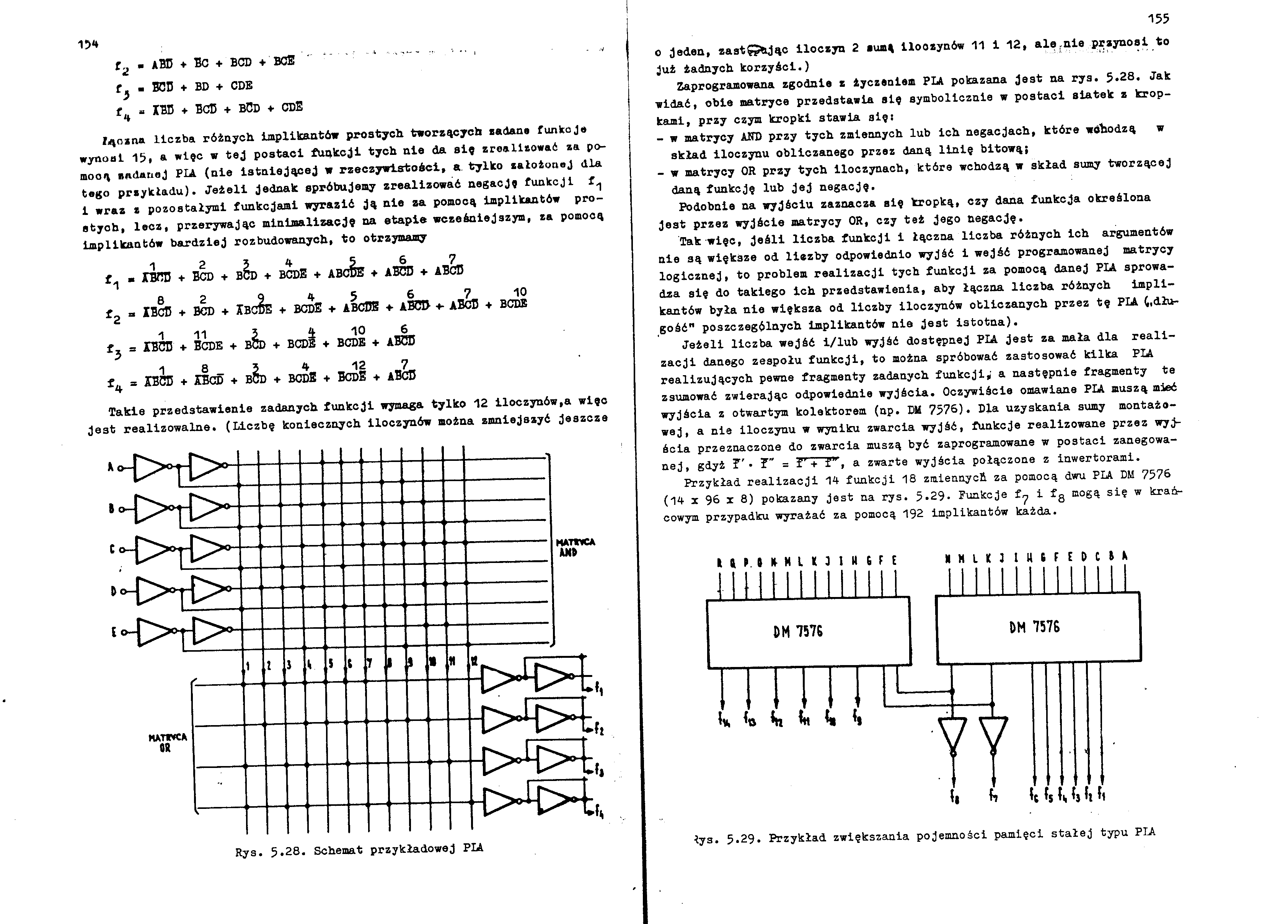
Rys. 5.28. Schemat przykładowej PU

o Jeden, zastęjhjąc Iloczyn 2 sumą lloosynów 11 1 12, ale.nie przynosi to Jul ładnych korzyści.)

Zaprogramowana zgodnie z tyczeniem PIA pokazana Jest na rys. 5.28. Jak widać, obie matryce przedstawia się symbolicznie w postaci siatek z kropkami, przy czym kropki stawia aięi

-    w matrycy ANS przy tych zmiennych lub Ich negacjach, które wchodzą w skład iloczynu obliczanego przez daną linię bitową;

-    w matrycy OR przy tych Iloczynach, które wchodzą w skład sumy tworzącej daną funkcję lub jej negację.

Podobnie na wyjściu zaznacza się kropką, czy dana funkcja określona Jest przez wyjście matrycy OR, czy też Jego negację.

Tak więc, Jeśli liczba funkcji 1 łączna liczba różnych ich argumentów nie są większe od liezby odpowiednio wyjść i wejść programowanej matrycy logicznej, to problem realizacji tych funkcji za pomocą danej PIA sprowadza się do takiego ich przedstawienia, aby łączna liczba różnych impli-kantów była nie większa od liczby iloczynów obliczanych przez tę PLŚ (.długość" poszczególnych Impllkantów nie Jest istotna).

Jeżeli liczba wejść i/lub wyjść dostępnej PIA jest za mała dla realizacji danego zespołu funkcji, to można spróbować zastosować kilka PIA realizujących pewne fragmenty zadanych funkcji,' a następnie fragmenty te zsumować zwierając odpowiednie wyjścia. Oczywiście omawiane PIA muszą mleć wyjścia z otwartym kolektorem (np. CU 7576). Ela uzyskania sumy montażowej, a nie iloczynu w wyniku zwarcia wyjść, funkcje realizowane przez wyjścia przeznaczone do zwarcia muszą być zaprogramowane w postaci zanegowanej, gdyż !"•?” = fTT, a zwarte wyjścia połączone z inwertorami.

Przykład realizacji 14 funkcji 18 zmiennych za pomocą dwu PIA DM 7576 (14 r 96 X 8) pokazany jest na rys. 5.29. Punkcje i f_g mogą się w krańcowym przypadku wyrażać za pomocą 192 Implikantów każda.

I I 1 łhMlKlIMGFE    NHLKltUSFCDCtś

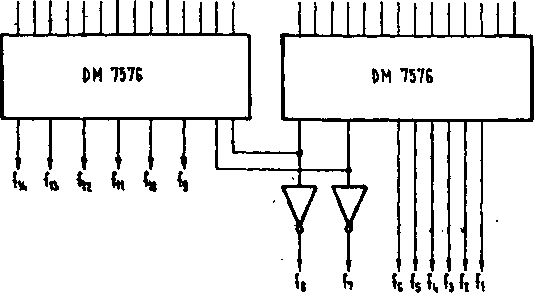
łys. 5.29. Przykład zwiększania pojemności pamięci stałej typu PIA