16299 skanuj0159 (2)

(odcinek Ccij). Od lego punktu przy zwiększaniu nakładów czynnika wytwórczego poza wielkość 0(" produkcyjność przeciętna będzie maleć. Produkcyjność przeciętna osiągnie zero. gdy produkcyjność całkowita będzie zerowa (spekulacja teoretyczna).

Jeżeli obliczy się dostateczną ilość przeciętnych produktów, można połączyć kolejne punkty «i. at itd. i otrzymamy ciągłą krzywą produkcyjności przeciętnej, jak to uczyniono na rysunku 8.6.

Podsumowując przeprowadzoną wyżej analizę, dotyczącą prawa wydajności nieproporcjonalnej, należy wskazać na pewne związki i zależności zachodzące między produkcyjnością całkowitą, przeciętną i krańcową. Ujmujemy je poniżej w cztery twierdzenia.

Twierdzenie 1

Gdy produkcyjność przeciętna wzrasta, produkcyjność krańcowa jest większa od przeciętnej (rys. 8.7).

f

0

Do C jednostek wytwórczych produkcyjność przeciętna wzrasta (w punkcie tym osiąga swe maksimum).

Miarą produkcyjności przeciętnej dla punktu H-. jest kar (z, utworzony z osią odciętych przez półprostą OK,, wychodzącą z początku układu współrzędnych.

Natomiast miara produkcyjności krańcowej dla punktu 5, jest kąt p. utwo rzony z osią odciętych przez styczną do krzywej produkcji w punkcie B_t. Ponieważ kąt .5 jest większy Cd kąta a aż do punktu C., produkt krańcowy jest większy od produktu przeciętnego aż do punktu C*.

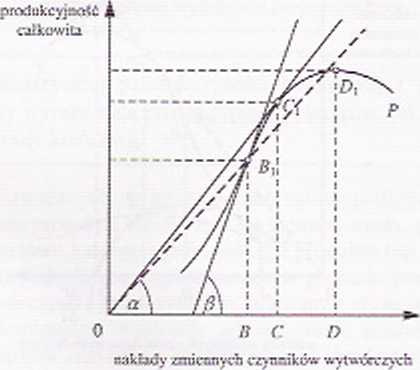
Rys.. S.7. Zależności między produkcyjnością przeciętną i krańcową