skanuj0023 (125)

Stwierdzono, że wyznacznik z macierzy przy niewiadomych jest różny od zera, wobec tego analizowany układ jest geometrycznie niezmienny (przy detA =0 układ geometrycznie zmienny).

Ponieważ zachowane jest kryterium ilościowe 2w = p+r (e = 31) to schemat jest statycznie wyznaczalny (5 W).

Dla analizowanego układu równań istnieje macierz odwrotna A~^l, istnieje zatem jednoznaczne rozwiązanie tego układu.

Pierwiastki równań wynoszą:

2_n R₂

R-2x ~ R-2y    “1" j    ~~'

&3x —    ~~    3

v* = \p₁₊\p»

t>2 = Pl+\P»

Kontrola poprawności rozwiązania.

EY = 0 V₁ + V_A+R₂y+R2_y—Pi = 0,

⁺ 2~^lr3^²~3*^>2~^^{1 =}

Znajomość siły D₂ (oraz reakcji) pozwala wyznaczyć siłę w pręcie Sj metodą przecięć.

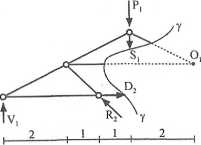
Suma momentów względem 0_lf (dla przekroju y—y) daje relację ZM₀₁ = 0,    -S₁*2-P₁-2~D₂-l + F₁+ó+R_2y*4 = 0,

fc = -^p^(^p^^p*)⁺³(i^p‘4^p>)⁺²i^p* n

= -Pi-lPiĄPi+lPi+PiĄPi- +2 Pr

Md,

Z analizy (tych tylko otrzymanych) wyników wnioskujemy, że przy obciążeniu tylko siłą pionową P_lt reakcje R₂ = R₂ = 0, a. siły występują tylko w prętach pasa górnego i dolnego. W przypadku obciążenia wyłącznie siłą poziomą P₂, występują siły we wszystkich prętach kratownicy.

Zademonstrowane podejście prowadzi wprawdzie do celu, ale jest uciążliwo (najlepsza metoda to metoda efektowna i efektywna). Zadanie to można rozwiązać stosując metodę wymiany prętów Henneberga, która pozwoli także określić geometryczną niezmienność układu.

Przekształćmy schemat kratownicy w łatwy do rozwiązania i na pewno geometrycznie niezmienny.

Przecinamy pręt D₂ (przyjmując w jego kierunku siłę X) i wstawiamy go w miejsce Z, otrzymując schemat o charakterze trójprzegubu.

2

2

2

02

• Oddziaływania:

ZM₀₂ = 0, Pi* %+R_2y'2+P_l -4-P₂ -4 = 0.

Przekrój I-I

ZM₁₂(0 = O, Pi • 2+U_2y • 2+Pj • 2-3T • 3-0, stąd 6V₁—6P_l—4P₂+3X = 0, V, = P₁₊łp₂-l_X,

6R₂,+12P,+4P₂-12X = 0,    P₂,= -₂P₁-|p₂+2^.

v,t

II

i *2    ■■■■ i 2    =—|

-i

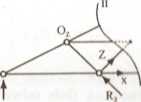
• Siła w pręcie Z kratownicy. Przekrój II—U

£M_0ł = 0,