16381 img457

lim

h * O

f(*o+h) -/(Ab) _L g(xo+h) - g(xo)

~T---⁺---T,-J ⁼

= /'(*o) +9'{xo).

|_)m /(*o^+h) ~ /(*>) + _Hm 9(><o+h) - g(x₀) /)-> O    h    h—yO    h

skąd wynika równość występująca w tej części tezy twierdzenia.

Ad c) Wzór ten wynika z dwóch poprzednich, jeśli uwzględnimy równość

f-g = f + [(-1) -g].

Ad d) Zauważmy, że:

_)im (f-9)(xo+h)-{f-g)(xo)-,_im [/(x₀+h)j • [g(x₀+h)] - [/(x₀)] ■ [g(x₀)j _ h—>0    h    ^ h—>0    h

z definicji iloczynu funkcji

₌ |_im \f(xp+h)] • \g(xp+h)] - [f(xo+h)] ■ g{xo) + f/(xb+h)] ■ g(xp) -[f{x₀)j • fcffe)] _ _t h^o    h

w liczniku dodajemy i odejmujemy [/(^o+ft)] •gfo)

^: lim

h^O

f(^xo + h)

g{x₀+h) - g(x₀)

+ g{*o) ■

f(x₀+h)-f(x₀)

Z założenia różniczkowalności funkcji / w punkcie x₀ wynika, na mocy twierdzenia 1., jej ciągłość w tym punkcie, skąd mamy:

lim f(x₀ + h) = f(xp).

Ponadto, wobec tego samego założenia oraz analogicznego założenia dla funkcji g, stwierdzamy, że istnieją skończone granice

lim

h-y O

f(xo+h) - f(xp)

f'(xo)

limSM4z5M _{= g}._(xo).

Korzystając teraz z twierdzeń o granicy: sumy funkcji, iloczynu funkcji oraz iloczynu funkcji przez stałą (twierdzenie 3. ze str. 1 7.), obliczamy:

lim

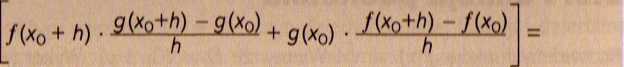
= /(*<o) • 9'(Xo) + /'(X₀) • 9(x₀), skąd wynika równość w tej części tezy.

Ad e) Dowód tej części twierdzenia pominiemy.

2.2. Pochodna funkcji w zbiorze

Przejdźmy teraz do różniczkowalności funkcji w niepustym zbiorze, który nie redukuje się do punktu. Określa ją następująca definicja.

DEFINICJA 5.

Funkcja / jest różniczkowalna w zbiorze A, jeśli jest różniczkowalna w każdym punkcie x₀ należącym do A.

Ta definicja wymaga komentarza. Najczęściej zbiorem A będzie pewien przedział liczbowy. Jeśli jest to przedział otwarty (a, b), to różniczkowalność funkcji / w tym przedziale oznacza jej różniczkowalność w każdym punkcie x₀e (a, b), czyli dla każdego x₀g (a, b) musi istnieć /'(x₀).

Natomiast jeśli zbiór A jest przedziałem domkniętym (a, b), to różniczkowalność w tym przedziale będziemy rozumieli w następujący sposób: dla każdego x₀e(a, b) istnieje /'(x₀), czyli funkcja jest różniczkowalna w przedziale otwartym (a, b) oraz dodatkowo istnieją skończone pochodne jednostronne f'+(a) i f'-(b). Podobnie określamy różniczkowalność funkcji w przedziałach (a, b) i (a, b).

Powiemy też, że funkcja jest różniczkowalna w przedziale (a, +oo), jeśli w każdym punkcie x₀e (o, +oo) istnieje /'(x₀) oraz dodatkowo istnieje skończona pochodna jednostronna f'+{a). Podobnie określamy różniczkowalność w przedziale (-°o. b).

Po tych wyjaśnieniach łatwo jest zrozumieć, co oznaczać będzie różniczkował ność funkcji w zbiorze A, który jest sumą przedziałów.