Dziawgo; Granice ciągów liczbowych 2

110 Granice ciągów liczbowych

_{g) lim}£^lM

ⁿ^°° 11 +1

3ⁿ⁺² _ 5.4^n+l

_C) Hm-    -j= ,

^n_>0° V4n + 6 -2vn

... 2n-lY'^+l d) lim - ,

ⁿ->°\ 2n +1)

Rozwiązanie:

Korzystamy z podstawowych twierdzeń dotyczących granic.

a)

h) lim

n-2 , o2n+2

ⁿ-»°° 3 • 2    + 2

3n - 2n +1

lim

ⁿ->°° n^/ + 2n - 3

co

co

n

= lim

n-»oo

f	2 1
3-	---^1--2
V	11 11

21 ,    2    3

n 1 +----

n n

.2 1 „ .. 2 _r 1 3---h — lim 3 - lim — 4- lim —

ri n² n->ro n->« n n-»oo ri

= lim---— =-t-— = 3

n->oo    2    3

1+ -n n

2    3

liml + lim— lim—

n->oo n—>00 ^ n->co

Dzielimy licznik i mianownik przez najwyższą potęgą mlii nownika.

Możemy też wyciągnąć nm wyższy stopień z mianowniku i licznika.

Granica ilorazu, to iloraz yia nic, a granica sumy (różno \ i to suma (różnica) granic (o IIp te granice istnieją).

b)

i 1 + 2 + 3+...+n n lim

n-rco\ n + 2    2

= lim

n->oo

(l + n)n n

2(n + 2)    2

= lim-

n—>oo

y z^n -r zj zy

n² + n-n² -2n

2(11 + 2)

|^oo — ooj =

i!S2(n + 2)

_1

2’

Wyrażenie w liczniku pierwsi <■ go ułamka jest sumą c/ąyii arytmetycznego.

(l + n)

1 + 2 + 3+...+n = --- n

2

Nie możemy rozbić granicy ną różnice granic, poniewnh otrzymalibyśmy symbol nu oznaczony

c)

lim

ⁿ^°° V4n + 6 - 2Vn

= lim

00 — 00

■yjĄn + 6 + 2 Vn

Aby policzyć tą granice należy pomnożyć i pod. w lić ułamek przez sprzężenie mianownika.

a/4ii + 6 +2Vn lim-:-:— = 00

(V4n + 6 - 2Vn)(V4n + 6 + 2Vn)

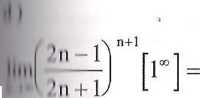
n+l

2n + 1 — 2^|

2n +1 J

Tym razem mamy do czynienia z innego typu wyrażeniem nieoznaczonym.

W obliczeniach wykorzystamy z własność zbież-

(    IV    (    1V

ności ciągu 1 + —    .    lim 1 H—    = e

v    n J    »->«v    n /

-2

n+1

lnu

2n +1

1

MIII

* "/'2n +1"'

^ V-2.....J

(

;2n+l\

t

2 n+l

2 n+l

'N -2

I i< lim

II >00

1 +

1

2n +1

= e.

V -2 )

lnu -(n + l) =-1 'ii i I ^v

Aby wykorzystać wzór . musimy najpierw wyrażenie w nawiasie zapisać w postaci /+.. . Następnie ułamek przekształcić w taki sposób, aby w liczniku była jedynka. Teraz musimy jeszcze odpowiednio zapisać potęgę. Robimy to w następujący sposób (wszystkie działania dotyczą potęgi):

1.    mianownik ułamka zapisujemy w potędze,

2.    zamykamy nawias kwadratowy,

3.    piszemy odwrotność tego co napisaliśmy w potędze,

4.    mnożymy przez dotychczasową potęgę.

(Potęga nie zmienia się, zmienia się tylko jej postać).

Korzystając z odpowiedniego twierdzenia o granicach ciągów otrzymujemy wynik.

| m ca il i;

n-1

3n-2

lilii

2n + 3

II |Mca')h:

Inn

11-1

2n+3

3n-2

lim

n->oo

= O

W tym przypadku nie mamy wyrażenia nieoznaczonego. Możemy od razu policzyć granice.

3n-2

2n

lim

II W

'O

1

(	n
1-
V	n j
( 1 1	\
1 1 k.	2 n >

V n;

(l+r

l 2n_y

3n-2

Możemy też granice tą policzyć w ten sposób, że z licznika i mianownika wyciągniemy wyrażenia z najwyższą potęgą.

Wiedząc, że granica iloczynu to iloczyn granic, rozbijemy granice na trzy.