20688 skanuj0007 (320)

59

Ćwiczenie 5

Przyjmując rozwiązania równań (5.4) w postaci drgań harmonicznych:

jc,(/) = 2Ą siniajj t + ó_t) x₂(t) = 2A₂ sin(co₂ t + ó₂)

(5.6)

(5.7)

-:żerny powrócić do naszych pierwotnych zmiennych (kątów <j>_{ i (p₂).

(p_l(t) = ~(x_] +JC₂)=4sin(w, t + d\) + A₂ sin(a>₂ / + <5₂)    (5.8)

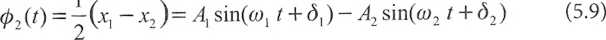
Otrzymaliśmy ważny wynik mówiący, że drgania oscylatora o dwóch stopniach r-wobody są superpozycją dwóch drgań normalnych (x_l5 x₂) o różnych częstościach własnych (o^, co₂), zachodzących jednocześnie.

Przedyskutujmy otrzymane wyniki dla wahadeł sprzężonych (rys. 5.2).

Jeżeli A₂ = 0, to </>, (t) = (p₂ (0 = Ą sin(cy, t + d_]) - oba wahadła drgają z tą samą częstotliwością w zgodnych fazach. Przypadek ten występuje, gdy oba wahadła początkowo wychylimy o ten sam kąt w tę samą stronę (oba w lewo lub oba w prawo). Wówczas sprężyna łącząca wahadła nie ulega rozciąganiu i na oba działają tylko siły grawitacyjne (patrz rys. 5.2a). Częstotliwość 0)j nie zależy od wielkości sprzężenia (położenia sprężyny a).

Jeżeli Aj = 0, to (p^t) = —</>₂(t) = A₂ sin(w₂1 + ó₂) - oba wahadła drgają z tą samą częstotliwością co₂ w przeciwnych fazach. Drugą postać drgań normalnych otrzymujemy, odchylając z pozycji spoczynkowej jednocześnie oba wahadła o ten sam kąt, ale w przeciwne strony (jedno w prawo, a drugie W lewo) i puSZCZa-jąc. Wówczas sprężyna łącząca wahadła jest raz kurczona, raz rozciągana (patrz rys. 5.2b). Występujące wówczas siły sprężystości powodują, że częstotliwość drgań obu jest większa niż w pierwszym przypadku drgania normalnego i wynosi co₂. Częstotliwość ta rośnie ze wzrostem sprzężenia.

Dowolna kombinacja dwu powyższych przypadków (ich superpozycja, czyli złożenie) daje postać ogólną ruchu dwóch sprzężonych wahadeł, co zapisaliśmy równaniami (5.8) i (5.9).

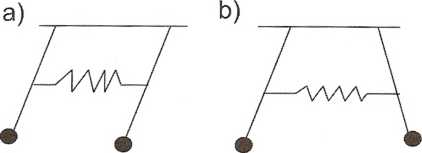
Rys. 5.2. Postacie ruchów dwóch sprzężonych wahadeł: a) drgań normalnych zgodnych w fazie; b) drgań normalnych o przeciwnych fazach; c) zapoczątkowanie zjawiska dudnienia

C)

/