skanuj0008 (308)

60

Ćwiczenia laboratoryjne z fizyki

Szczególną postacią możliwych zachowań rozpatrywanego układu (badaną w ćwiczeniu eksperymentalnie) są dudnienia. Powstają one gdy odchylimy z pozycji spoczynkowej tylko jedno z wahadeł o pewien kąt (patrz rys. 5.2c), po czym puścimy je. Odpowiada to sytuacji gdy Aj - A₂ = A, ój = ó₂ - 0. Równania ruchu wahadeł (5.8) (5.9) dla dudnień przyjmują wówczas postać:

01 (0 = A cos ² ₂ ⁰⁾¹ t j cos    t j = A cos (gW^os (a)J)    (5.10)

0₂ (0 = -dsinf'⁰⁾² ₂ ⁰⁾¹ /jsinf^¹ *^<°²1) = A sin (ft^/jsin (a)_srt)    (5.11)

gdzie: (O_mod

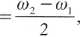
w_sr

tWj +co₂ 2

Każde z wahadeł wykonuje drgania z częstotliwością    równą średniej arytme

tycznej częstotliwości drgań normalnych i amplitudą zmieniającą się z częstotliwością modulacji (o_mod. Przebieg wahań obu wahadeł przedstawia rys. 5.3. Ponieważ oba sprzężone wahadła są identyczne, energia zawarta w pierwszym (wychylonym na początku) wahadle będzie poprzez sprężynę przekazywana do drugiego, aż do chwili gdy się ono zatrzyma, a z amplitudą początkową będzie poruszać się tylko wahadło drugie. Pełen okres dudnień T_d zakończy się, gdy ponownie zatrzyma się drugie wahadło. Wahadła wymieniają się energiami z częstością dudnień dwa razy większą od częstotliwości modulacji:

(o_d—o)₂ C0j    T_d —    (5.12)

©a

Celem ćwiczenia jest doświadczalne sprawdzenie teoretycznej relacji (5.12) oraz na bazie zależności (5.5) wyznaczenie stałej sprężyny k. Ze zmianą stopnia sprzężenia wahadeł (zmianą położenia sprężyn a względem osi obrotu wahadeł) zmienia się również częstotliwość drugich drgań normalnych i częstotliwość dudnień. Na podstawie zależności (5.5) funkcja (o\ = f{a²) jest linią prostą:

(o²2=(o²x+—^a²    (5.13)

ml

W równaniu tej prostej y = Ax + B wyraz wolny B jest równy kwadratowi częstotliwości pierwszego drgania normalnego a współczynnik nachylenia A zależy od stałej sprężystości k.