22018 skanuj0112 (25)

204

Ofeślar

^R^^s- S_s_ -I

^ V

~n

\

''iNP 220

V. Zginanie ukośne_

Funkcje momentów zginających.

Ze względu na siłę „P” w punkcie B wprowadzamy granicę przedziału obciążenia. Odcinek AB - z e (0;0,25l)

M_x(z)= Ra_v z - Ó,5qz² = 0,5qlz - 0,5qz²;

Mx(0)“0;    M_x(0,25l)= ^ql².

My = 0.

Odcinek BC - z e (0;0,75l)

M(z)= Rcy -z - Q,5ą£ = 0,5qlz - 0,5qz²;

M(0)=0;M(0,75I)= ±ą\².

Mj = 0.

Maksymalny moment zginający równa się:

M„,« = M(0,5I)=

Określamy momenty zginające od siły „P” (rys. 5.5.2b).

Z równań równowagi ^M_y_ = 0 i ]TM_y = 0 otrzymujemy:

Rax = 0,75P,    Rcx m 0.25P.

Pozostałe reakcje są równe zeru.

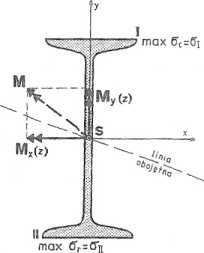
Rys, 5.5.3

Funkcje momentów zginających. Odcinek AB - z e (0;0,25l)

M_y(z)= R_Ax z = 0,75Pz;

M_y(0)=0, M_y(0,25l) m 0.1875PI.

M_x = 0.

Odcinek BC - z e (0:0,751) M_y(z)=RcxZ = 0,25Pz;

M_y(0)=0,    M_y(0,75l)= 0.1875PI.

M_x = 0.

Określenie największego naprężenia normalnego.

Położenie wektorów momentów zginających M_x(z) i M_y(z), w dowolnym przekroju poprzecznym belki przedstawiono na rys. 5.5.3.