24854 P1010815 (2)

262

<u RAMY 2BUETOWB

II, METODY OIUCŻIŃ I KONSTRUKCJA

263

Należy wspomnieć tu o artykule prof. dra B. Bukowskiego „Uproszczone obliczy żelbetowych ustrojów ramowych*', opublikowanym w Inżynierii i Budownictwie, bj7 1954 r, Dla typowych schematów ram istnieją gotowe zbiory rozwiązań, które ’ T.nalcźó w tablicach i podręcznikach inżynierskich. Ostatnio dużą popularnością ciei się metoda Crossu, bazująca na metodzie deformacji. Wyższość tej metody w zastouo*_a mu praktycznym nad metodami klasycznymi polega na szeregu ułatwień i oproszą rachunkowych. Poza tym wszelkich operacji obliczeniowych dokonujemy na samej ram_!t a nie zajmujemy się rozwiązaniem równań wielu niewiadomych, wymagąjących nierai bardzo żmudnych wyliczeń.

W aacgólności wybór metody będzie zależeć od decyli konstruktora, jak i od rodzaju ramy. Warto nadmienić, że dla wszystkich ram przesuwnych i nieprzesuwnycb o rozpo. rach prostych najwygodniej stosować metodę Crossa, a do ram o rozporach załamanych lub łukowych metodę sił.

Ze względu na szerokie stosowanie metody iteracyjnej Crossa-Błaszkowiaka celowe będzie przypomnienie kilku zasad ułatwiających rozwiązania układów ciągłych lob ra-■owych.

1. Obliczenie sztywności i współczynników rozdziału z powodu przejrzystości rachunku zaleci się przeprowadzać tabelarycznie, jak w załączonym przykładzie.

1 \v obliczeniach w miarę możności należy wykorzystać symetrię układu oraz symetrię lub antysymetrię obciążenia. Pizy symetrii układu i obciążenia rozróżniamy dwa przypa-dot

a)    oś symetrii przecina przęsło,

b)    oś symetrii pokrywa aę z prętem lub przechodzi przez węzeł.

Gdy oś symetrii piżama przęsło, wtedy sztywność tego przęsła przyjmujemy za równą połowie sztywności podstawowej; wtedy S=2EI/L Natomiast gdy oś symetrii przechodzi przez węzeł, to pręty schodzące się w nim rozpatrujemy jako całkowicie zamocowane. Pizy symetrii układu i antysymetrii obciążenia też rozróżniamy dwa przypadki:

a)    oś symetrii przecina przęsło,

b)    oś symetrii pokrywa się z prętem lub przechodzi przez węzeł.

Gdy oś symetrii przecina przęsło, to sztywność tego przęsła przyjmujemy za równą pół-torakrotnsi sztywności podstawowej; wtedy S=6E7//. Gdy oś symetrii pokrywa się z prętem, to sztywność słupa znajdującego się na osi symetrii przyjmujemy za równą połowie sztywności rzeczywistej.

Jeżeli rozpatrujemy belkę wiełoprzęsłową o parzystej liczbie przęseł, możemy podzielić ją na dwie oddzielne belki, przy czym pręty, zbiegające się w węźle znajdującym się na osi będą miały sztywność równą 3/4 sztywności podstawowej i wtedy S-lEl/l,

Obliczenia dla ramy obciążonej anty symetrycznie przeprowadzamy podobnie, jak przy obciążeniu symetrycznym tylko dla połowy ustroju, dla drugiej połowy otrzymamy wyniki symetryczne i znaki momentów przywęzłowych będą identyczne. Natomiast przy obciążeniu symetrycznym znaki momentów dla drugiej połowy będą przeciwne.

3. Zaleca się również podział momentów przywęzłowych przeprowadzać tabelarycznie, przy tym dogodne jest stosowanie zapisu uproszczonego, to jest przy węźle równoważnym zapisywanie jedynie momentów przekazanych, a dopiero w przedostatnim wierszu tablicy zapisywanie podziału cumy rozdzielonych momentów.

Zasady wyżej omówione zostały zastosowane przy rozwiązaniu ramy piętrowej w przyjdzie liczbowym.

przystępując do obliczenia statycznego ramy należy przeanalizować możliwości radego rodzaju uproszczeń, jak założenie przegubów rzeczywistych lub plastycznych, wyko-^•stanie symetrii i antysymetrii obciążeń.

Przy obliczaniu ram żelbetowych można korzystać z następujących uproszczeń:

1.    Jeżeli rozpiętości przęseł ramy wiełoprzęsłowej różnią się do 10%, ramę można _tozwiązać jako równoprzęsłową, przyjmując do obliczeń średnią wartość rozpiętości przęseł.

2.    Ramę o rozporach pochyłych, których nachylenie do poziomu jest mniejsze niż 1/8 można liczyć .jak ramę o rozporach poziomych, przyjmując do obliczeń średnią wysokość słupów.

3.    Dla uzyskania symetrii obciążeń dopuszczalne są pewne przesunięcia sił działających na ustrój. Przesunięcie siły może być jednak nie większe niż 5% rozpiętości przęsła, w którym siła działa.

4.    W przypadku działania na rozporę skomplikowanego układu obciążeń dopuszczalne jest zastąpienie go układem prostszym. Musi być jednak spełniony warunek, by wykresy momentów od rzeczywistego i zastępczego układu sił, jak dla belki wolno podpartej, nie różniły się więcej niż 5 %. Uproszczenie to jest szczególnie ważne przy stosowaniu gotowych wzorów do obliczania ram.

Z wyżej wymienionych uproszczeń nie można korzystać w przypadku, gdy zastosowanie każdego z nich działa w tym samym kierunku, to jest zmniejsząjąco lub zwiększająca

6,1.1. Przybliżone obliczanie układów ramowych na obciążenie pionowe

Statycznie niewyznaczalne ramy i budynki szkieletowe wymagają przy rozwiązywaniu ich dużego nakładu pracy.

W pewnych przypadkach możemy korzystać z przybliżonych metod. Przybliżenie polega na tym, że dla obciążenia pionowego rozpatrujemy pewien wycinek ramy (rys. 6.1),

Rys. 6.1. Schematy fragmentarycznego obliczania ram na obciążenia pionowe

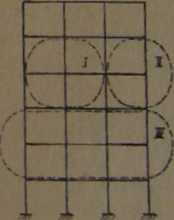
uważając skrajne pręty takiego wycinka za utwierdzone całkowicie (pomijając faktyczne utwierdzenie sprężyste) oraz przyjmując ów wycinek za ustrój nieprzesuwny.

Wycinki takie można szybciej obliczyć niż cały ustrój szkieletowy. Przy obliczeniach układów o prętach prostych najwygodniej jest stosować metodę Crossa.