ekonomia (26)

68 II. Metody i narzędzia analizy ekonomicznej

270°-360°. Ponieważ. Ig a> Ig «'(gdyż a>a'), krzywa na rys. II.8 ma w punkcie A nachylenie większe niż w punkcie U.

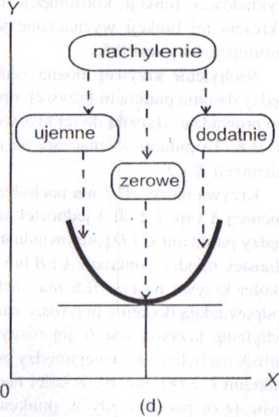
Rysunek 11.9 przestawia przykłady różnych nachyleń prostych i krzywych.

Y

V

{ nachylenie') -l nieskończone/

0

(a)

X

(b)

X

y

^ nachylenie^)
f dodatnie ^V-1-^ :C^zer	1 A_ ( ujemne ) / ^ 1 □we ^ i
i ' _J	L i
f	A - X

Rys. 11.9. Przykłady nachylenia linii prostych i krzywych

Nachylenie krzywej w danym punkcie można też mierzyć obliczając pochodną odpowiedniej funkcji w tym punkcie⁷.

Nachylenie nie jest jednak wyznaczone jednoznacznie przez stromość prostych czy krzywych, czyli kąt, jaki proste lub styczne do krzywych tworzą z osią odciętych. Kąt ten zależy też bowiem od skali wykresu (innymi słowy od tego, jak duże czy małe jednostki oznaczamy na osiach współrzędnych). Oto przykład: na rys. II. 10 mamy

Y    Y

Rys. 11.10. Identyczna wartość nachylenia dwu prostych o różnym kącie nachylenia

dwie linie proste mające nachylenie o tej samej wartości liczbowej, dokładnie I/2, ale jedna z nich jest o wiele bardziej stroma niż druga. Wynika stąd wniosek, że różnice w' stromości prostych czy krzywych są w' pchli porównywalne (i wskazują jednoznacznie na różnice w' nachyleniu) dopiero przy takiej samej skali na osiach współrzędnych porównywanych wykresów.

W kwestii zastosowania pochodnej (i w ogóle rachunku różniczkowego) w ekonomii patrz np.: Podstawy ekonomii. Ćwiczenia, zadania, problemy, wyd. 2, Warszawa 1999. zwłaszcza rozdział pierwszy.