31628 S6303021

414 hydraulika techniczna, przykłady obliczeń

_ F _ ma ^F F' m'a^f

t __t_

t    /'

4    1

= <*_P<*L —

a.

(15.10)

Proporcję (15.9) można przekształcić, aby otrzymać po obu stronach równania elementy należące do jednego układu:

Wyrażenie to nosi nazwę liczby Newtona (wartość niemianowana). Dla uzyskania podobieństwa dynamicznego liczba Newtona Ne musi być jednakowa dla obu porównywanych układów.

Uzyskanie pełnego podobieństwa dynamicznego (tzn. w stosunku do wszystkich sił) spełniłoby wymagania idealnego modelowania obiektów hydrotechnicznych. Jednak realizacja tego warunku w stosunku do wszystkich możliwych rodzajów sił jednocześnie jest tak trudna, że w praktyce badań niemożliwa do osiągnięcia. Przy przepływach cieczy mamy do czynienia, oprócz sił bezwładności, z siłami ciężkości, tarcia, sprężystości i napięć powierzchniowych. Każda z tych sił wiąże się w inny sposób z wymiarami układu, czasem i właściwościami fizycznymi cieczy. Zwykle jednak dość łatwo można ocenić wpływ poszczególnych sił na przebieg zjawiska i zrezygnować, bez widocznego wpływu na wynik badań, z odwzorowania części z nich na modelu. Jeśli uznać któryś z rodzajów sił czynnych za dominujący w zjawisku, wystarczy, aby stosunki tych właśnie sił i sił bezwładności były sobie równe.

Podobieństwo sił ciężkości - kryterium Froude'a

Siła ciężkości Fc zależy od masy cieczy i działającej na nie jednostkowej siły masowej g. Skala sił ciążenia jest więc równa:

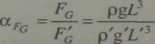
= °pW

3

(15.12)

Dla osiągnięcia podobieństwa dynamicznego skala sił ciężkości musi być równa skali sil bezwładności. Warunek ten można więc zapisać w postaci (porównaj równanie 15.10):

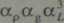
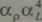
2

(15.13)

a,

(15.14)

(15.15)

lub uwzględniając równanie (15.9): pg£³ _ pL²v²

p'g'L'³ p'L' V²

Po uporządkowaniu zależności (15.14) i redukcji otrzymano:

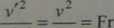
g'L'

projektowanie parametrów geometrycznych i hydraulicznych fizycznego modelu 415

Wartość —- = Fr jest bezwymiarowa i nazywa się ją liczbą Froude’a.

i!

Według kryterium podobieństwa Froude’a (15.15), dwa układy podobne geometrycznie i kinematycznie, w których dominującą jest siła ciążenia są podobne również dynamicznie, gdy liczba Froude’a jest jednakowa dla układu modelowego i naturalnego.

Z warunku równości liczby Fr dla dwóch układów wynika wiele bardzo ważnych zależności, a mianowicie skale podobieństwa poszczególnych elementów ruchu cieczy na modelu i w naturze.

Aby wyprowadzić związki skal poszczególnych wielkości fizycznych w warunkach stosowania kryterium Froude’a, porównano wyrażenia określające skale sił bezwładności i sił ciężkości:

(15.16) a/

Przyjmując stałą jednostkową siłę masową na modelu i w naturze, tzn. g^{/ =} g (ct_g = 1)

______I

oraz wykorzystując tę samą ciecz na modelu i w naturze, tj. p=p' (a_p = I), otrzymano zależność określającą skalę czasu:

a, =a¹/²    (15.17)

Związek ten pozwala na wyznaczenie pozostałych skal w funkcji skali długości a_L, a mianowicie:

skala prędkości:	ot/ a, i/2 av =—=—77r=a/ a, a^1/^2	(15.18)
skala przepływu:	^aG p ^av% j§ 0Cl^/2«ł 2 Al	(15.19)
skala siły:	ctF =apagaj =a^2 (przyjmując ap =1 i ag =1)	(15.20)
skala ciśnienia:	CLp 'A = —= -y = ctL i| K	(15.21)
skala spadków:	Otf= 1 (gdy wymiary liniowe w obu układach nie ulegają zmianie)	(15.22)
skala pracy:	<%; =aFaŁ=aJaŁ=“l	(15.23)
skala mocy:	a ^aL ^ai -a» i 1 a, a^1/^2 1	(15.24)

W ten sposób wyprowadzono związki skal podstawowych dla badań hydraulicznych wielkości w warunkach przyjęcia kryterium podobieństwa Froude’a. Warto zwrócić uwagę na fakt, że skala czasu i prędkości są sobie równe, spadki w naturze i na modelu fizycznym są identyczne, natomiast prędkości maleją na modelu wolniej w stosunku do