37670 skanuj0003 (230)

- 90 -

Załóżmy, iż w chwili początkowej (t =0) kąt skręcenia cewki galwanometru wynosi oraz że w chwili tej przez galwanometr przestaje płynąć prąd elektryczny. Równanie (8.7) dla 1=0 możemy po niewielkich przekształceniach zapisać w postaci:

- 90 -

da

2/3

da

(8.11)

gdzie w r/^D/I oznacza tzw. Jczęstotliwość rezonansową galwanometru,

'o 2I(R+R T

oznacza |współczynnik tłumienia, /3_q= f/2I - współczynnik tłumienia w warunkach, w których cewka pomiarowa ma rozwarte końce (wówczas występuje tylko moment sił tłumienia mechanicznego M_m , a nie występuje moment mechaniczny sił oporu "indukcyjnego" ).

Równanie (8.11) jest klasycznym równaniem opisującym drgania harmoniczne tłumione. Jego rozwiązanie należy osobno rozpatrywać w warunkach tzw. słabego 2 2 2 2

( (*>_o > fi ) i silnego (    < /3    ) tłumienia. W pierwszym przypadku

rozwiązanie równania (8.11) ma postać:

a = a_Qe ^^tcos wt ,    (8.13)

gdzie

“ = /“o-P^{Z = ?}T    ^<8-¹⁴>

o/nucza częstotliwość przemiennych skręceń cewki galwanometru, T - okres tych drgań, a_Q - skręcenie początkowe.

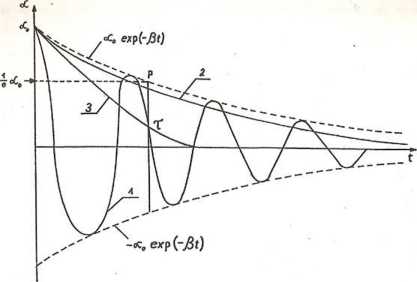
Rys. 8.3. Zmiany w czasie wychylenia plamki świetlnej galwanometru przy powrocie do poiożenia zerowego (1    - ruch tłumiony

pseudookresowy, 2 - ruch aperiodyczny, 3 - ruch krytyczny)

Ruch cewki w warunkach słabego tłumienia jest ruchem tłumionym pseudookresowym (krzywa 1 na rys. 8.3). Amplituda    wychyleń w tym ruchu

maleje w czasie zgodnie z zależnością:

a. = a e'¹⁵¹    .    (8.15)

Logarytm naturalny stosunku amplitud dwóch kolejnych drgań określa tzw. dekrement logarytmiczny zaniku (tłumienia) amplitudy drgań

a (t)

° ^{= ln} a.(t+T)

= ln e

0T

0 T

(8.16)