38082 Image25

48

1.14

a. Przyspieszenie punktu poruszającego się po okręgu wyraża się za pomocą współrzędnych biegunowych przez wektor

r(p² t_r + rę t

a = a_r i_r + dy i_v =

gdzie i_r i i są wektorami jednostkowymi tego układu

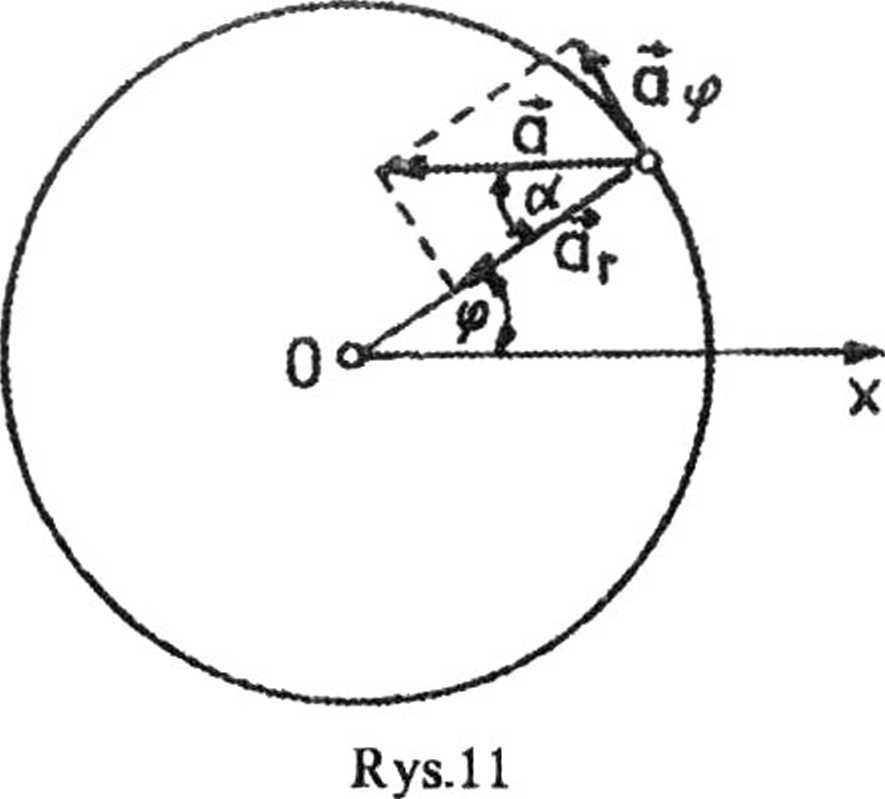
Z rys. 11 widać, że

a

<p _

a.

= tga.

Podstawiając do tego wzoru odpowiednie

wartości na a₉ i a_r otrzymujemy

<P

J¹

= tga,

co można też zapisać w postaci

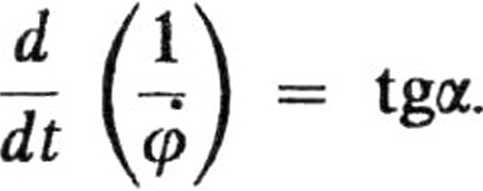
Po rozdzieleniu zmiennych i scałkowaniu mamy

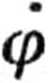
1 + t (d₀ tga'

Całkując ponownie znajdujemy szukany kąt

<P

ctga ln | (1 + t qj₀ tga)|.

Gdy a n

“ = 2* ⁹ b.

= 0, prędkość kątowa ę = const, czyli ruch jest jednostajny. Gdy = 0, więc nie ma ruchu.

r co

v = r (p

t

gdzie tj = 1 + t co₀ tga.

Zaznaczone na rys. 12 współrzędne prostokątne x, y związane są z współrzędnymi biegunowymi v, t_i równaniami: x = v cost_l> y = v sint_A.

L i

Wzór przedstawiający równanie hodografu jest równaniem spirali hiperbolicznej. Jej asymptota znajduje się w odległości y — rco₀ od osi x (rys. 12), gdyż

lim y = lim v sint_l

sin t_i

lim r m-

t, —* o

t j -*o

ti-* o

t

= r(0₀.

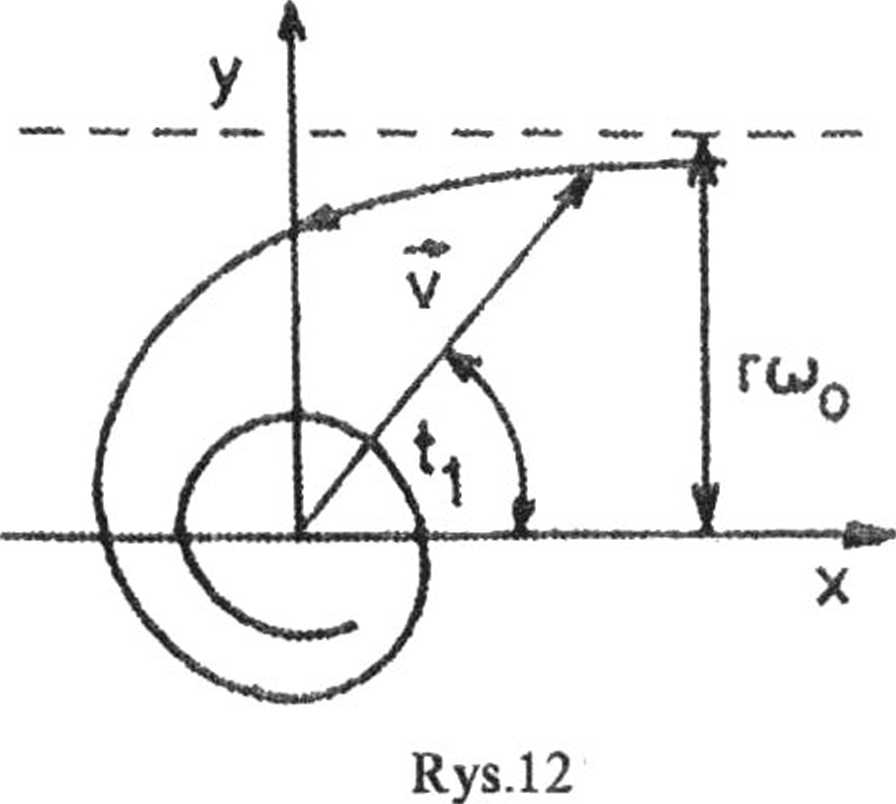
.15. Różniczkując dane równanie dwukrotnie względem czasu otrzymujemy

• •

2 axx + bx = 1,

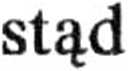
Stały punkt ma więc współrzędną b

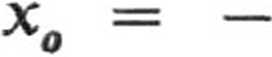
2a

1

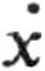
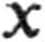
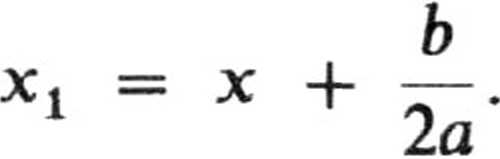
2ax + b*

2ax^{1 2} -f 2axx -f bx = 0,

więc

1

2

4a²x\ ’