40445 Untitled Scanned 18

- ustaleniu zapisu algebraicznego w postaci sumy implikantów prostych albo iloczynu implicentów prostych, odpowiadającego wybranemu zestawowi grup jedynek albo zer.

Przykłady wykorzystania tablic Kamaugha pokazano na lya 2.2 i 2.3.

Metodę Kamaugha praktycznie stosuje się do syntezy funkcji o najwyżej sześciu argumentach.

2.3.2. Metoda Quine’a-McGuskeya

Metoda Quine'a polega na:

-    wykonaniu wszystkich możliwych sklejeń w postaci kanonicznej danej funkcji, co oznacza znalezienie wszystkich prostych implikantów albo wszystkich prostych implicentów tej funkcji,

-    wyborze minimalnego zestawu prostych implikantów albo prostych implicentów.

McCluskey zmodyfikował metodę Quine»a przez wprowadzenie cyfrowego zapisu toku przekształceń.

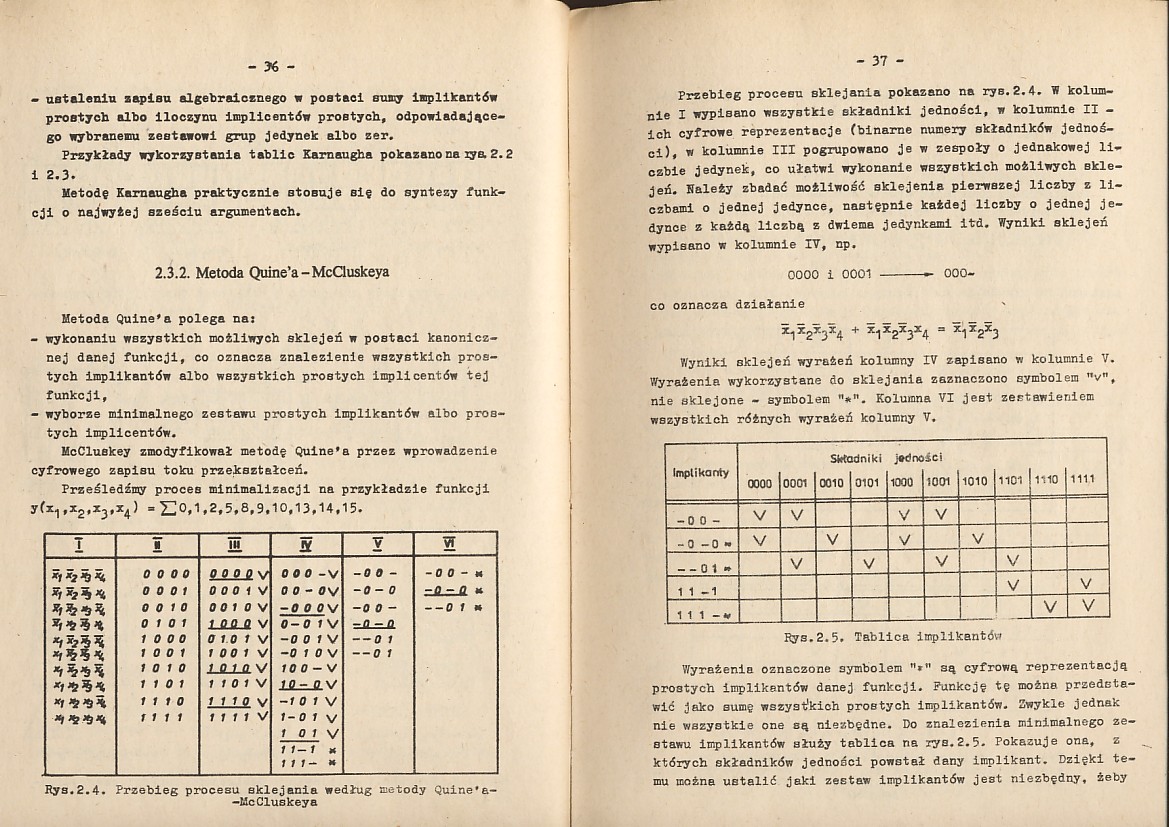
Prześledźmy proces minimalizacji na przykładzie funkcji

»*2^,x3»		x4) -Eo.1	,2,5,8,9.	10,13,14,	15.
	T	¥	M	5	V	w
	*1*2*3*.	0 0 0 0	0-0.0-g V	0 0 0 -V	-0 0-	-0 0 - u
	*1*2*S*.	0 0 0 1	0 0 0 1 V	0 0 - <?v	-0-0	zsi.-.a. *
		0 0 10	0 0 1 0 V	-0 0 0 v	-0 0-	--0 f M
		0 10 1	1 fl-fl.-fl V	0-0 1\/	zJL.-a
		10 0 0	0 1 0 1 V	-0 0 1 V	--0 1
		10 0 1	1 0 0 1 V	-0 / 0 V	— 0 1
	*1*2*3*%	10 10	JSLUL V	10 0 - V
	*1*2%*	110 1	1 1 0 1 V	1.0 - 0 V
	*1 *2*i\	1110	1 1 1 o V	-1 0 1 v
	*1*2^*%	1111	1 1 1 1 v	f- 0 1 V
				1 o i v
				/ /- f X
				1 1 1 - »

Rys.2.4. Przebieg procesu sklejania według metody Quine'a-

-McCluskeya

Przebieg procesu sklejania pokazano na rys.2.4. W kolumnie I wypisano wszystkie składniki Jedności, w kolumnie II -ich cyfrowe reprezentacje (binarne numery składników Jedności), w kolumnie III pogrupowano Je w zespoły o jednakowej liczbie Jedynek, co ułatwi wykonanie wszystkich możliwych sklejeń. Należy zbadać możliwość sklejenia pierwszej liczby z liczbami o jednej Jedynce, następnie każdej liczby o jednej Jedynce z każdą liczbą z dwiema Jedynkami itd. Wyniki sklejeń wypisano w kolumnie IV, np.

0000 i 0001 -- 000-

co oznacza działanie

Wyniki sklejeń wyrażeń kolumny IV zapisano w kolumnie V. Wyrażenia wykorzystane do sklejania zaznaczono symbolem V, nie sklejone - symbolem    Kolumna VI Jest zertawieniem

wszystkich różnych wyrażeń kolumny V.

Implikonty	0000	0001	Sktc 0010	kdniki 0101	jedno 1000	ści 1001	1010	1101	1110	1111
-0 0 -	V	V			V	V
> o 1 o 1	V		V		V		V
- - 0 1 -		V		V		V		V
1 1 -1								V		V
1 1 1 -V									V	V

Rys.2.5. Tablica implikantów

Wyrażenia oznaczone symbolem są cyfrową reprezentacją prostych implikantów danej funkcji. Funkcję tę możne przedstawić jako sumę wszystkich prostych implikantów. Zwykle jednak nie wszystkie one są niezbędne. Do znalezienia minimalnego zestawu implikantów służy tablica na rys.2.5. Pokazuje ona, z których składników jedności powstał dany implikant. Dzięki temu można ustalić jaki zestaw implikantów jest niezbędny, żeby