40708 str051 (3)

Ocena dokładności wyznaczenia pozycji

Dokładność określenia pozycji w systomi" < <I’N im i/nn określić poprzez macierz kowa-rlonc|l wektora przyrostu współrzędnych Madei/ kowariancji wektora losowego X o postaci

ogólnej

~X,

x =

4.87)

X.

będącego realizacją wielowymiarowej zmiennej losowej (X_v X₂.....X„) -jest macierzą o nastę

pującej postaci:

= E

c	J,=£{x-£(x)][X-£(xf }=
'X,-E(XJ
x2-E(x2)	[Xl-E(Xt) X2-E(X2) ..., X1-E(X1)\
[xn-E{X,X

Ąxt - E(x, )f} E$x, - E(Xt )][*, - E{X2)]} , £(*,)][*,-£(xj £|Z2-£(X3)]^2}		... Eix,-E{Xx)][X,-E{Xl)\ ... £{[Z2-£(X2)IX„-£(XJ]} =
* % 1	£(X,)]} E{Xm -E(X„)[X2-E{X2)}}	£|x -£(X )]^2} .
_	V(Xl) COv(Xi,X2) ... cov(X2,X{) V(X2) ...	cov(Xt,XnJ cov(X2,Xj	(4.88)
	cov(Xn,Xi) cov(X,„X2)	v(xj .

I 'ortleważ

cov

cov{x,,Xj)- -£’(x,)][x_j -£'(x_j)]}= £{[Xj -■£'(x_j)][X_l -£'(X_j)]} =

Ąx_Jtx,),

/ulem macierz C_x jest macierzą symetryczną. W jej skład wchodzą wariacje - V(X„) na przekątnej oraz kowariancje - cov(X„,X„) poza nią.

lilii

Waklor przyrostu współrzędnych pozycji w nynttmiln (łl'N \ /doflnlownno jako

X ■ [A<p AX A/i Afl„ |' ,    (4.90)

gdzie:

A<p - przyrost wektora stanu w kierunku N-S,

A\ - przyrost wektora stanu w kierunku E-W,

Ali - przyrost wektora stanu w kierunku wertykalnym,

A8„ - przyrost błędu zegara odbiornika.

Dla otrzymania macierzy kowariancji wektora X skorzystajmy z zależności (4.88) otrzymując

F(A(p)	cov(A(p,A^)	cov(Acp,A h)	cov(A(p,A8„)
cov(AA.,A(p)	v(ax)	cov(AA,, A h)	cov(AA.,A8„)
cov(Ah, Acp )	cov(A/i, AX)	V(A h)	cov(a/?,A8„)
cov(A5„,A(p)	cov(A8n, A\)	cov(A80,A/j)	Kas0)

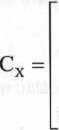
Zgodnie z przytoczoną definicją macierzy kowariancji, w przypadku nawigacyjnego ro/wlg; u nia GPS, jej przekątna zawiera wariancje odpowiednio zdefiniowanych przyrostów s/inoki>ś< i geograficznej, długości geograficznej, wysokości oraz błędu zegara odbiornika 1’o/nstnlo pola macierzy to kowariancje wspomnianych zmiennych. Macierz kowariancji wektora X rozwiązania nawigacyjnego pozycji w systemie GPS, w funkcji liczby wykorzystywanych salo iitów, można zapisać w oparciu o macierz G jako:

dla liczby satelitów n > 4

(4.92)

C_x = (GTC)-¹ G^tC_l G(G^tG)-¹ ,

gdzie:

C_L - macierz kowariancji wektora pomiaru o postaci

C_L =

^(pi) cov(p„p₂)

^cov(p₂,P,) v(p₂)

coyfo.pj"

^cov(p₂,p„)

(4.03)

y(pj

(4.94)

_cov(p„_>Pl) cov(p„,p₂) oraz dla klasycznego rozwiązania n = 4

C_x = G‘C_lG-^t

w którym przez analogię

C_L =

r(p.)	cov(p,,p2)	cov(p2,p3)	cov(pi, p4)
cov(p2,p,)	v(p2)	cov(p2,p3)	cov(p2,p4)
cov(p3,p,)	cov(p3,p2)	y(pj	Tl- CL > o o
cov(p 4, p|)	cov(p4,p2)	cov(p4,p3)	V(pJ _

(4.95)

107