42015 str162 (3)

162 3. PRZEKSZTAŁCENIE LAPLACE’A I JEGO PEWNE ZASTOSOWANIA

Rozwiązanie. Transmitancja K(s) określona jest zależnością

(1)

gdzie

K(s) =

U₂(s)

u^y

l/₁(s) = L[«₁(0]    i U₂(s) = L[n₂(t)] .

Transformatą sygnału wejściowego jest funkcja

(2)

C/,(s) = L[f²] =

Po uwzględnieniu wyrażenia (2) w zależności (1) otrzymujemy transformatę sygnału wyjściowego

t/₂(s) = /C(s)[/₁(s) =

4

s³(s + 3) ‘

Transformata napięcia zasik

(2)

Transformatę natężenia prąc

(3)

W zależności od wartości s²LC+sRC+l może mieć: a miejsca zerowe, c) dwa mii każdy z wymienionych prz;

Przypadek a). A = R²C

(1)

Z twierdzenia Borela (o transformacie splotu) możemy napisać

L^_1 [K(s) t/i(s)] = | u_l(z)k(t—z)dz = 2}T²e”^(,_t,dt = o    o

= 2e~'\z²e^xdz = 2«"(tV-2te‘ + 2e‘-2), o

zatem

u₂(t) = 2(t²—2t+2—2e~‘).

Zadanie 4.13. Obwód elektryczny przedstawiony na rysunku 3.5 został zamknięty w chwili t = 0, zatem dla t>0 w obwodzie tym płynie prąd elektryczny /(/) ze źródła o stałym napięciu u(t) = U₀ = const. Wyznaczyć przebieg natężenia prądu i(t) dla obwodu znajdującego się w stanie nieustalonym. Przyjmujemy, że kondensator znajdujący się w obwodzie był rozładowany dla 0.

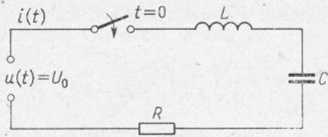
Rys. 3.5

Rozwiązanie. Impedancja operatorowa rozważanego obwodu wynosi

Z(p) = R+jL + —.

(4)

Wyznaczamy obecnie orygin

*(o= i

k — 1 s

I

= lim -

5“+Sl 5

U₀

L(s_t

gdzie , s₂ są określone wzi Przypadek b). A = R²

(5)

Natężenie prądu i(t) w obwi i(t) = res [/ (.s) e'¹] =

5 = JO

gdzie s₀ jest określone wzon Przypadek c). A = R²C

(6)

ii*