str168 (3)

168 3. PRZEKSZTAŁCENIE LAPLACE’A I JEGO PEWNE ZASTOSOWANIA

Rozwiązanie. Stosujemy przekształcenie Laplace’a do obu stron równania, jako funkcji zmiennej t. Mamy wtedy

(3)    L[/(f) + 3y(0] = L(5/² + 3t+4).

Stosując wzór (1.6) do obu stron równania (3), mamy

(4)    L[/(r)] + 3L[y(t)] = 5L(/²) + 3L(/) + 4L(l).

Zgodnie z wzorem (1.7) mamy

(5)    L[/(0] = SL[y(0] —y(+0).

Uwzględniając związek (5) we wzorze (4) i biorąc pod uwagę warunek (2), mamy

(6)    SL [y (t)] + 3L [y (!)] -1 = 5L (t²) + 3L (f) + 4L (1).

Z tablicy przekształceń, § 8, otrzymujemy

(7)

M*²) = Jj, = ^L(D = ^-.

Uwzględniając związki (7) we wzorze (6), mamy po przekształceniach

L(y) =

(8)

S³ + 4S² + 3S+10

(S+3)S³

Rozkładamy prawą stronę (8) na ułamki proste:

(9)

_ 10 1    1    1    37 1

^L(j) ~ J"Śⁱ~J"s^{2 +} 2l' ~S

10 1

27 S + 3'

Biorąc po obu stronach równania (9) odwrotne przekształcenie Laplace’a, mamy

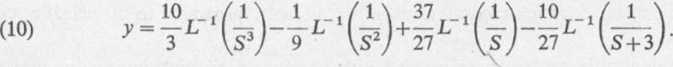
Korzystając z tablicy przekształceń otrzymujemy

,, _ 5,2 J, , 3 7 _ 10-3/ f-3¹ _9‘+27    27^e

Zadanie 5.2. Rozwiązać równanie

(1)    y"(0-y'(0-2y(0 = l,

przy warunkach początkowych

(2)    y (0) = l,    y'(0) = o.

Rozwiązanie. Stosujemy przekształcenia Laplace’a do obu stron równania (1), jako funkcji zmiennej t. Mamy wtedy

(3)    L[y''(0-/(0-2y(0] = Ł(D-

Stosując do lewej strony (3) wzór (1.6), mamy

(4)    L(y"(0)-L(y'(0)—2L(y) = L(l).