60476 str192 (3)

192 3. PRZEKSZTAŁCENIE LAPLACE'A I JEGO PEWNE ZASTOSOWANIA § 6. WYZNACZANIE

Rozwiązanie. Aby znaleźć rozwiązanie ogólne danego układu wprowadzamy warunki początkowe

(2)    y(0) = C₁₁ z (0) = C₂,

gdzie C_t oraz C₂ oznaczają stałe dowolne.

Stosujemy następnie do każdego równania układu (1) obustronnie przekształcenie Łapiące^. Korzystając z jego liniowości, otrzymujemy wtedy

₍₃₎    L(/)+L(z) = L(<²)+6L(0+L(1),

L(z') — L(y) = — 3L(t²) + 3L(f)+L(l).

Na mocy wzoru (1.8) mamy

₍₄₎    L(y') = SL(y)-y( + 0),

L(z') = SL(z)-z(+0).

Uwzględniając w układzie (4) warunki początkowe (2), mamy

₍₅₎    L(/) = SL(y)-C₁,

L(z') = SL(z)-C_z.

Z tablicy przekształceń Laplace’a odczytujemy

(6)

L(l)=i,    L(0=^r,    L(t²) = ^.

Podstawiając wzory (5) i (6) do układu (3) otrzymujemy po przekształceniach i uporządkowaniu

(7)

SL(y) + L(z) = ^3 + ^2 + Y ^{+ Cl} ’

-L(y)+SL(z)= -^ + -₂ + j + C₂.

Rozwiązując układ (7) względem niewiadomych L(y) oraz L(z) otrzymujemy

L(.y) =

1

1-C₂ c,s

(10) z = 2L~¹

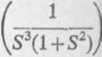
Stosując twierdzenie Bor< wyliczamy kolejno

(U)

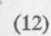
(13)

L_

\s³(l+s²)

(-L,

\S(1 + S-

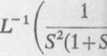
(8)

L(z) =

S³(l + S²) S²(l + S²) S(l + S²)    1+S²    1 + S²

2    4

1 + Cj    C₂S

+

S²(l + S²) S(l + S²)    1 + S² 1 + S²'

Stosując do każdego równania układu (8) odwrotne przekształcenie Laplace’a i wykorzystując jego liniowość, otrzymujemy

^{y 6L} (s³(l+s²)) ^L (s²(1 + S²)) ^{+ 5L} (s(l + s²))⁺

+(! - C₂) L-¹ (j^) + C.L"¹ (i-^i).

(14)

Podstawiając wzory (11), (li ogólną układu (1)

(15)    ^{y = 3t} z = t²

Uwaga 1. Znajomość ca różniczkowych) pozwala ro; równań).

Uwaga 2. Rozwiązanie gdy wartości funkcji i jej poci rozwiązania przy warunkach

Zadania do rozwiązania

1. Znaleźć rozwiązanie o

a)    y”'-3ay"+3a²y'-a³y

b)    y"'—2y"—3y'+ 10y =

c)    4y⁽⁴⁾ — 12/" +1 ly" - 3.

13 — Wybrane działy matematyki..

(9)