42505 Untitled Scanned 32 (8)

Ostateczny wykres momentów będzie więc sumą tylko M_p i M₃X₃.

.    1 ql ql²

m$x₃=—/—=—;

3 12    36

b 2 ql ql

m!x₃=—i—=—.

3    12    18

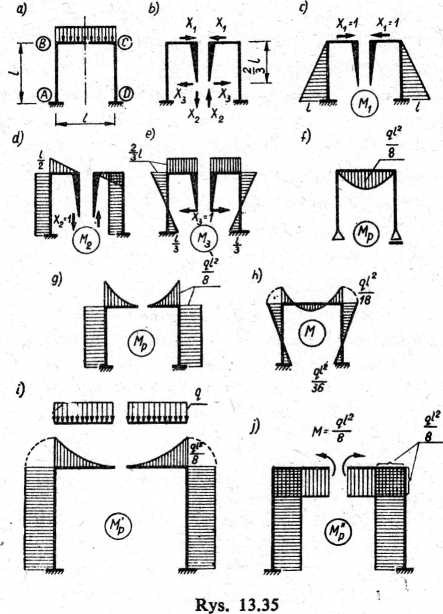
Wykres sumaryczny momentów widzimy na rys. 13.35h. Jeżeli dla M„ przyjęlibyśmy taki sam układ zastępczy (rys. 13.35g) jak dla wielkości nadliczbowych, to obliczenie tej ramy przebiegałoby następująco:

wartości zerowe przyjmują te same przemieszczenia jednostkowe co i w układach poprzednich, z wyjątkiem A_lp\

1    1,1 ql

A_3pEJ=2- — — ---1+2-— • — ■/—/ --2----/—r—=—_qf.

382*3    23    38    233 1,8    72

Układ równań kanonicznych przybiera postać:

Sn Xi + A_lp = 0Szz 2^2 = 0;    S₃₃X₃ + A_3p=0.

1 ql² 1    2    1    2    2 qt²

0B)

470