43113 PC043385

82

. a Ject Siała (por. ilustracja 1.37).

y v=b	i ■ (0 J>)
	X

Przykład 1.74

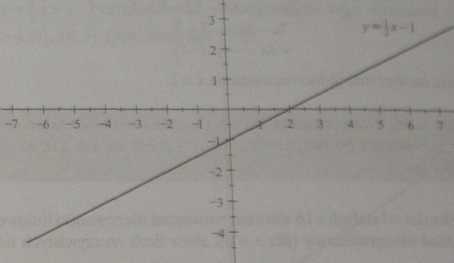
Funkcja /(x)=ix-l, której wykres znajduje się na ilustracji 1.38, jest rosnąca w zbiorze R. Ponieważ yx-l = 0<=>x = 2, funkcja posiada miejsce zerowe

aZa "^*^ŁfeS ^^Un^' przecina oś Ox pod kątem ot, takim że tg a = ^. Wykres qi przecina oś Oy w punkcie (0,-1). Funkcja przyjmuje wartości ujemne dla xe (-x,2) i dodatnie w zbiorze (2,co).

Ilustracja 1.38. Wykres funkcji liniowej f (*) = .! _x -1

Równania i nierówności liniowe z jedną niewiadomą

Definicja 1.65. Równaniem liniowym z jedną niewiadoma x nazywamy równanie postaci ax + b = 0, gdzie a,be R.

W zależności od stałych a i b równanie liniowe może mieć jedno rozwiązanie (równanie oznaczone, dla a * 0), nieskończenie wiele rozwiązań (równanie tożsamościowe, dla a = 0 i b = 0) lub nie mieć żadnego (równanie sprzeczne, dla a = 0 i b = 0).

Rozwiązywanie równania liniowego polega na jego równoważnych przekształceniach poprzez wykonywanie następujących operacji:

-    dodawanie do obydwu stron lub odejmowanie od obydwu stron równania tych samych wyrażeń (przenosimy jednomiany ze zmienną* na jedną stronę równania oraz wyrazy wolne na drugą i redukujemy wyrazy podobnej.

-    mnożenie lub dzielenie obydwu stron równania przez taką liczbę (różną od 0), aby współczynnik przy niewiadomej * wynosił 1.