PC043380

1

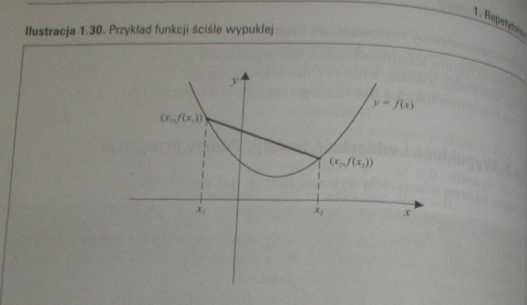
Ilustracja 1.31. Przykład funkcji ściśle wklęsłej

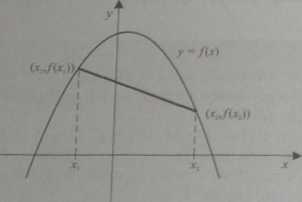
Uwaga 1.28

a)    Funkcja/jest ściśle wypukła w przedziale (#,&) wtedy i tylko wtedy, gdy jej wykres leży ponad wykresem stycznej dla każdego punktu z przedziału (a,by

b)    Funkcja /jest ściśle wklęsła w przedziale (a,b) wtedy i tylko wtedy, gdy jej wykres leży pod wykresem stycznej dla każdego punktu z przedziału {a,b). \

Definicja 1.58. Punkt (^{1 2}„./(,t₀)) diax_(l e Uf nazywamy punkiem funkcji /, jeśli jest ona wypukła (wklęsła) w lewostronnym sąsiedztwie t„ i wklęsła (wypukła) w prawostronnym sąsiedztwie x„.

U Uwaga 1.29. Punktem przegięcia jest więc taki punkt wykresu funkcji, w którym styczna przechodzi z jednej strony tego wykresu na drugi (por. ilustracja 1 ..12).

Ilustracja 1.32. Punkt przegięcia wykresu funkcji

O

Uwaga 1.30. Metoda wyznaczania przedziałów wypukłości i wklęsłości oraz punktów przegięcia wykorzystuje pojęcie drugiej pochodnej (por. podfozdz.

7.3.2).

1

Przykład 1.64

Funkcja / przedstawiona na ilustracji 1.33:

•    jest ściśle wypukła w przedziałach: (-«►, |§) oraz (x,,»),

•    jest ściśle wklęsła w przedziale (x_ux₂),

2

   ma punkty przegięcia w punktach o współrzędnych: (z,,/(ż₃)) oraz