00098467

150 II. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE

Na przykład funkcja f(x) •= e' jest analityczna w dowolnym otoczenia punktu *₀    0, po-

150 II. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE

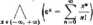
Def. Funkcję Ax,y) nazywamy analityczną w otoczeniu Q punktu -P₀(*<>; >o)» jeżeli

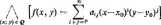
Można udowodnić, że funkcja analityczna w otoczeniu Q punktu P_Q ma w tym otoczeniu pochodne cząstkowe dowolnego rzędu, a ponadto dla każdej pary (i,J) nieujemnych liczb całkowitych

_ 1 _

“ i! j! dzfdyi

Szereg potęgowy dwóch zmiennych (11.17) jest wówczas szeregiem Taylora funkcji Ax,y).

Na przykład funkcja f(x, y) = sin(a+>) jest analityczna w dowolnym otoczeniu Q punktu (0; 0), ponieważ

(i+;)*

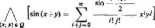
Podobnie definiujemy pojecie funkcji analitycznej trzech lub większej liczby zmiennych niezależnych.

Podamy teraz bez dowodu zapowiedziane wcześniej dwa twierdzenia Cauchy’ego-Kowalewskiej odnoszące się odpowiednio do równania (11.12) oraz do równania (11.14).

Tw. 1. Jeżeli:

\° funkcja f,(v, ,v₂, ...,t'₆) Jest analityczna w pewnym otoczeniu punktu (x₀;

To w *2 ;■*?;*«) eślj,

2" funkcja <p{y, z) jest analityczna w pewnym otoczeniu punktu (y₀; Zo) -e Di. to istnieje otoczenie punktu <x₀; y_a; z„) e D,, h> klórym zagadnienie Cauchy'ego dla równania (11.12) ma dokładnie jedno rozwiązanie analityczne.

Tw. 2. Jeżeli:

funkcja f₂(v_t,t>₂,...,v_IB) jest analityczna w pewnym otoczeniu punktu

(żoiy&l f-Oi fol tjJ ...j Xjg) EŚłj,

2" funkcje tp(y,z,t) i y(y, z, l) są analityczne w pewnym otoczeniu punktu (Po.Zo.foJeDJ,

to istnieje otoczenie punktu (x₀; J>₀1 ^zo i *o) ^E D* ■^w którym zagadnienie Cauchy’ego dla równania (11.14) ma dokładnie jedno rozwiązanie analityczne.

Uwaga. Niech będzie dane równanie różniczkowe cząstkowe rzędu pierwszego

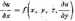
w którym u - u(x,y) jest funkcją niewiadomą, a JXVi,Vt, vj,o«) jest Funkcją daną określoną w pewnym obszarze SI ^c E*.

Zagadnienie Cauchy'cgo dla tego równania w prostokącie P:a < x<b, c<y<ti polega na wyznaczeniu takiego rozwiązania u — ti(x, y), które spełnia warunek początkowy ufx₀,y) - p(y)

przy czym liczba r_D e <fl, 6> oraz funkcja y(.y) określona w przedziale <e, rf> są z góry dane. Zagadnienie to ma prostą interpretację geometryczną. Chod2i mianowicie o wyznaczenie takiej po-wierzchni całkowej u - u(x, y) danego równania, która przechodzi przez z góry daną krzywą

.*-*>, U = f(y), ye (c, d)    (11.18)

Bardzo często zagadnienie to formułuje się w ogólniejszej postaci. Chodzi wówczas o wyznaczenie powierzchni całkowej danego równania przechodzącej przez krzywą

* = *<»),    y->(«).    «“«(<).    »e(ó,0)    (11.19)

która nie zawsze leży w jednej płaszczyźnie.

Może się zdarzyć, że przez krzywą (IL1S) lub (11.19) przechodzi nieskończenie wicie powierzchni całkowych równania. Krzywą taką nazywamy wówczas charakterystyką tego równania.

ĆWICZENI ó

1.    Jakie równanie nazywamy równaniem różniczkowym cząstkowym? Podać definicję: a) rzędu, b) całki szczególnej, c) całki ogólnej równania różniczkowego cząstkowego.

2.    Na czym polega zagadnienie Cauchy’ego: a) dla równania różniczkowego cząstkowego rzędu pierwszego, b) dla równania różniczkowego cząstkowego rzędu drugiego?

3.    Sformułować twierdzenia Cauchy’ego-Kowalewjkiej dla równań (11.12) i (11.14).

,—    du

4.    Wykazać, że funkcja u = pary jest rozwiązaniem szczególnym równania «(ztS) --- —

-y(yrw) — “ 0 w dowolnym obszarze płaskim zawartym w zbiorze D — {(.{; y):.ry> 0). dy

x    du    du

5.    Wykazać, że funkcja u = — jest rozwiązaniem szczególnym równania xy---y⁷ ~—x

2y    dx    dy

w dowolnym obszarze płaskim zawartym w zbiorze D ** )(*; y)\y i= 0).

6.    Znaleźć równanie różniczkowe o pochodnych cząstkowych rzędu pierwszego z funkcją

Wskazówka. Obliczyć pochodne — i —, a następnie z otrzymanych równań wyrugować funkcję /•

7. Znaleźć równanie różniczkowe o pochodnych cząstkowych rzędu drugiego z funkcją niewiadomą tt(x,<), które ma w dowolnym obszarze płaskim rozwiązanie postaci: a) u “•/(*)sln»+£(x)casf, b) u    c) u ~ f{xĄ-l)+g(x—t), gdzie / i g są to do

wolne funkcje klasy C^J w przedziale (-od, +03).