str206

206 4. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE RZĘDU DRUGIEGO

Ponieważ(p(/) jest dowolną funkcją, zatem możemy u(x, y) zapisać w następującej postaci:

(10)    u(x,y) = F(x)+A(y)e?ⁱ-F(0),

gdzie F(x) jest dowolną funkcją różniczkowalną. Obecnie tak dobieramy funkcje F(x) A (y), ażeby były spełnione warunki (2). Z drugiego warunku mamy

u (0 ,y)'=F (0) + A (y) - F (0) = 3y^:5,

⁽¹¹⁾    >4(y) = 3y³, natomiast z pierwszego warunku otrzymujemy

u(x, 0) = F(x)+A(0)e^xi-F(0) = 5x*+x²,

⁽¹²⁾    F(x)—F(0) = 5x⁴+x².

Uwzględniając zależność (11) oraz (12) w wyrażeniu (10) określającym ogólne rozwiązanie u(x, >), otrzymujemy rozwiązanie równania (1) spełniające warunki (2). Jest to funkcja następującej postaci:

u (x, y) = 5x⁴+x² + 3y V³.

Zadanie 1.6. Wyznaczyć ogólne rozwiązanie równania

3. Wyznaczyć ogólne roz d²z

a)

+ 4x = 0,

8xdy

8²u du ^c> =

dx dx 4. Wyznaczyć rozwiązani; d²u

a)

dxdy 8²u d²u 8x8 y⁺dy

2x sin y = 0, u (

b) —+ —, = 0, u(x,C

c)

8²u 8u

= 0, u(x,0)

8x8y 8y 5. Wyznaczyć ogólne roz

a)

8²u

8x8y

—2 xz = 0,

(1)

I

d²u

8xdz

—4xzy^s = 0.

Rozwiązanie. Całkujemy obie strony równania (1) względem zmiennej z i stąd mamy

(2)

-—2xz²y^s = ę>(x,y),

gdzie cp jest dowolną funkcją dwóch zmiennych całkowalną względem zmiennej x.

Obecnie całkujemy obie strony równania (2) względem x i stąd otrzymujemy ogólne rozwiązanie równania (1)

u(x,y,z) = x²y^sz²+F(x, y)+G(y,z),

gdzie F i G są dowolnymi funkcjami klasy C² dwóch zmiennych.

Zadania do rozwiązania

1.    Sprawdzić, czy funkcja u = xe^xy jest rozwiązaniem równania różniczkowego

8u 8u

2.    Sprawdzić, czy funkcja z = sin(x—y) jest rozwiązaniem równania różniczkowego

, 8²u    -__

x²—i~^x y—+y—. = o.

2.8 Z 2 ^c dx^{2 + X}

8²z 8z 8z --hy—by — = 0.

8x8 y ^y 8x ^y dy

Odpowiedzi

1.    Tak.

2.    Tak.

3.    a) z(x,y)=-x*y+F

b)    z(x,y) = A(y)e~^x-

c)    u(x,y) = A(y)e?~

d)    M(x,y) = F(y)+G|

4.    a) w(x, y) = x²(2-coj c) u(x,y) = e^xy¹+x³

5.    a) m(x, y, z) = x²yz+ b) u(x, y, z) = x²y²z^l

§ 2. Klasyfikacja rówm . i ich postać kanon

Definicja 1. Równaniem wiadomej funkcji u(x,y) dw stępującej postaci:

(2.1)

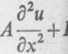
gdzie A, B,C, a, b, c, d są dat w pewnym obszarze płaskin