str242

242 4. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE RZĘDU DRUGIEGO I 8. ROZ

Uwaga. Własność 1 dotyczy również szeregów (8.7).

Przykładem ciągu ortogonalnego z wagą w przedziale (0, a) jest ciąg utworzony z funkcji Bessela, np.

(8.9) ^Jp(^^1;C)’ ^Jp(^a^X'}' ^p>-1,

gdzie y„ są kolejnymi dodatnimi pierwiastkami równania J_p(y) = 0 lub też J'_p(y) = 0. Własność 2. Wagą ciągu funkcyjnego (8.9) jest

e(x) = x.

Definicja 10. Szeregiem Fouriera-Bessela funkcji f(x) w przedziale (0, a) nazywamy szereg (8.7), gdzie

Xn(x) = Jp(^x'j, p>-1.

Rozwiązywanie równań różniczkowych cząstkowych liniowych za pomocą przekształceń Laplace’a polega na transformowaniu względem jednej ze zmiennych niezależnych wyraz po wyrazie składników równania, a następnie rozwiązywanie już dowolną metodą uzyskanego w ten sposób równania różniczkowego przy transformowanych warunkach granicznych. W ten sposób znajdujemy transformatę funkcji i po dokonaniu transformacji odwrotnej otrzymujemy funkcję szukaną. Transformacji równania różniczkowego dokonujemy względem tej zmiennej niezależnej, od której nie zależą współczynniki występujące w danym równaniu.

Zadania przykładowe

Zadanie 8.1. Wyznaczyć rozwiązanie u(x, t) równania przewodnictwa dla §<x<a i t>0

d²u 1 du

⁽¹⁾ 8x² = 7 ~dt ’

spełniające następujące warunki graniczne:

u(x, 0) = u_o>0, dla 0<x<a, lim u(x,i) = 0

u(0, t) = u(a, 0 = 0 dla f>0.

Rozwiązanie. Poszukujemy ciągu rozwiązań u„(x, t) równań (1) w postaci (5) “nC* , 0 = X„(x) T„(t) .

Funkcje X„(x) i T„{t) dobieramy w ten sposób, ażeby funkcja u„{x, t) spełniała równanie (1). Pochodne funkcji (5)

d²u. _____ ____ du„

~dt

podstawiamy do równania

którą wobec założenia u„(>

(7)

Jeżeli ^„(a) i T„{t) będ;

(8)

to funkcje (5) będą spełnia (9) :

Całkami ogólnymi równań

(3)

(4)

Z warunków brzegowyc *„(0) = A Rozwiązanie równania (

(10) u(>

gdzie D_n = B„C„. Funkcja

Współczynnik D_n wyznaczar u(x, 0) = u₀, zatem

D„ są współczynnikami w na uogólniony szereg Fouri

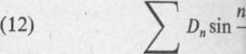
n=l

—i = T„(t), — = X_n(x) T„'(r)

(6)

16"