20883 str212

4. RÓWNANtA RÓŻNICZKOWE CZĄSTKOWE RZĘDU DRUGIEGO 212 5 2. KLASY

Zadanie 2.4. Sprowadzić do postaci kanonicznej następujące równanie różniczkowe:

(1)

ó²u

- + x

,d²u

₂du -y t- = o.

dxdy ' dy^{2 J} dy

Rozwiązanie. Obliczamy wyrażenie 5 dla określenia typu danego równania 5 = B²—4AC = 4x²y⁴—4x²y⁴ = 0.

Równanie (1) jest zatem typu parabolicznego. Piszemy obecnie równanie różniczkowe charakterystyk

w-

2xy^2<^-+x² = 0, dx

Zadanie 2.5. Sprowadzić

(1)    9y

Rozwiązanie. Obliczam

(2)    5 = i

Równanie (1) jest zatem typu i terystyk

skąd mamy

(2)

dy x

Tx ⁼ 7‘

Rozwiązaniem równania (2) jest następująca rodzina charakterystyk:

3x² —2y³ = C.

Dla sprowadzenia równania (1) do postaci kanonicznej przechodzimy do nowych zmiennych ć i 4 (2.14), określonych następującymi zależnościami:

(3)    £ = 3x²—2 y³,    rj = x.

Obliczamy obecnie współczynniki A_x, B_x, C_t, a_x i b_x w równaniu otrzymanym z równania (1) po przejściu do zmiennych £ i ą (3):

A_x = B_x — 0,

,2    a„ a„ za„\2

d²d d²d e²ę dd, dd

+ C ~ «“ł* ci ——f- b —— —

' dx²    dxdy    dy² ’ dx    dy

= 6y⁴—l2x²y—6y⁴ = -12 x²y,

d²tj    d²t]    d²r\ dr]    dt]

b\ = A—^ + B

+ C ——, + a ——h b —— = 0.

~dx² ' “ dxdy ' ^wdy² ' dx dy

We współrzędnych d i t] równanie (1) przyjmuje następującą postać kanoniczną:

,d^zu    ₂du

y³-₂- 12x²- = 0. dt\    dd

Współczynniki występujące w powyższym równaniu wyrażamy również w zależności od zmiennych d i rj posługując się wzorami (3)

d²u „ du

du

skąd mamy

(3)

Rozwiązaniem równania (

Dla sprowadzenia równai zmiennych d i t] (2.15) okres

(4)

Obecnie obliczamy wspólc

b_x = A

We współrzędnych d i i] rów

(5)

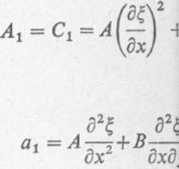
Końcową postać zależnośi ków (4) i podstawieniu do zi

i