str248

248 4. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE RZĘDU DRUGIEGO

Całkami ogólnymi równań (10) są funkcje

X_k(x) = A_k cos K_kx + B_k sin K_kx, YJy) = C_m cos M_my + D_m sin M_my, Z_n(z) = E„ cos N_nz + F_n sin N_nz, T_km„(t) = G_kmn cos A_kmnvt+H_kmn sin k_kmnvt.

Z warunków (4) otrzymujemy

kn

Xk( 0) = A_k = 0, X_k(a) = B_ksinK_ka = 0, K_k = —,

następnie z warunków (5) mamy

Y_m(0) = C_m = 0,    YJh) = D_m sin    = 0, M_m =

mn

i z warunku (6)

mc

Z„(0) = £:_I1 = 0,    Z„(c) = F„sinN„c = 0, N„ = ~.

Obecnie korzystamy z warunku początkowego (3) i dlatego obliczamy pochodną

TL_n{t)

T_kmn(t) = -    G*_m„ sin    + X_kmnv H_km„ cos A*™®!,

T_kmn(0) — Kmn°Hkmn — 0 >

gdzie

A*_m„t>* 0, zatem H_kmn = 0.

Obecnie funkcję u(x, y, z, /) możemy zapisać w następującej postaci, przyjmując ⁼ Bk^mFifiknin-

\    OO    CO    00

kroć    miry    mtz

Imn sin-Sin —- sin-cos l._kmnvt,

a b c

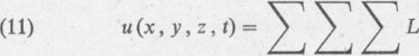
k= 1 m=1 n= 1

gdzie zgodnie ze wzorem (9) mamy

(12)

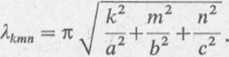
Funkcja (11) spełnia warunki brzegowe (4), (5) i (6) oraz warunek początko.wy (3). Wartości współczynników L_kmn wyznaczamy z warunku początkowego (2), skąd mamy następującą zależność dla 0<x<a, 0<y<h i 0<z<c:

(13)

CO    OO

. knx . inny    nnz

L_kmn sm-sin —- sin-

a b    c

U₀.

\

k = 1 rri = 1 n = 1