str260

260 4. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE RZĘDU DRUGIEGO

§ 8. ROZV

Zgodnie ze wzorem (9) szukana funkcja u(x, t) jest następującej postaci:

‘

x    2U₀ \ ¹ ( — 1)* . hix    ( k²n² \

U(x,t)=U₀—+- } —-—sin-exp(--_rt).

a    k / i k a    \    a )

k — \

Zadanie 8.9. Wyznaczyć funkcję spełniającą równanie fali płaskiej

d²u 1 d²u

7²

oraz następujące warunki graniczne:

0)

dx²    c² dt²

natomiast z warunku (8) w

Transformata szukanej 1

(2)

(3)

(4)

m(x,0) = ^—^ =0 dla 0<x<a,

dla f>0,

u(a,ł) = U_o>0 dla t>0.

Rozwiązanie. Dokonujemy transformacji Laplace’a obu stron równania (1) względem zmiennej t, oznaczając

U(x ,s) — L, {u (x, 0}.

otrzymujemy

1    s

~2 ^₍(x ,0)    j

c    c

d²U s² c

Po uwzględnieniu w równaniu warunków początkowych (2) mamy

d²U s²

(6)

Obecnie transformujemy warunki brzegowe (3) i (4)

(7)

(8)

U(a,s) = -U₀. s

Rozwiązujemy obecnie równanie różniczkowe (6) uwzględniając przy tym warunki (7) i (8). Całką ogólną równania (6) jest funkcja

s    s

U(x, s) = ylcosh — x + £sinh—x.

c    c

Z warunku (7) otrzymujemy

(9)

Dla otrzymania oryginał funkcji U(x,s). Biegunami

oraz

jt(2

s* =—

Wszystkie bieguny funkc obliczamy z następującego '

u(x,t) =

liczymy zatem residua wystt

u_k(x,t)= r

c

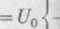
H