46865 skanuj0078 (36)

Rozdział 7. ❖ Analiza matematyczna 93

Ćwiczenie 7.5. —

Oblicz całką jln xdx-1

1. Wywołaj operator całki oznaczonej, wpisz granice, funkcję podcałkową i zmienną całkowania. Naciśnij znak równości (rysunek 7.21).

Rysunek 7.21.

Całka oznaczona

f^e

ln(x) dx = 1 ^jł

Ćwiczenie 7.6. —*■

Oblicz całkę

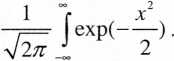
1. Dla większej wygody zdefiniuj wyrażenie podcałkowe jako funkcję zmiennej x i nadaj jej nazwę Gauss (rysunek 7.22).

Rysunek 7.22.

Definicja funkcji Gauss

Gauss(x)

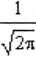
exp

V ² /

( 2\

-x

2. Wywołaj operator całki oznaczonej, wpisz do niego funkcję podcałkową Gauss oraz zmienną całkowania. Wpisz granice dolną i górną. Do uzyskania symbolu nieskończoności wykorzystaj albo skrót klawiszowy Ctrl+Shift+Z, albo odpowiednią ikonę z paska narzędzi Calculus (rysunek 7.23). Następnie wpisz znak równości (rysunek 7.24).

mm'

*

1" S n ! ? ¥

Rysunek 7.23.

Ikona symbolu nieskończoności na pasku narzędzi Calculus

Rysunek 7.24.

Gauss(x) dx = 1

Całka oznaczona w granicach niewłaściwych